論文番号 １ 著者名 藤井信太郎，福島雅紀，郭 文秀，京藤敏達，西村仁嗣 論文題目 緩勾配方程式のグリーン関数および一般解の導出 討論者 磯部雅彦（東京大学） 質疑 水深変化のある場合のヘルムホルツ方程式の係数は，水深変化がない場合には方向θに無関係であるのに対し，θの関数となる．この場合には，０次のハンケル関数のみならず，１次以上の高次のハンケル関数を使って解が表される．このような級数解と，この論文でのべき級数解とはどのような関係にあると考えられるか． 回答 水深変化がある場合，波数kがθに依存するためグリーン関数もθの関数となります．水深変化がない場合においても，θ依存性がある１次以上のハンケル関数を用いて表現される解は，波源強度の算定が不可能な真性特異点を持ちます．したがって本研究のグリーン関数の導出では，０次のハンケル関数と同様に除去可能な特異性logrを持つ級数式（７）を仮定し，その係数pn，qnにおいて水深変化，つまり波数kのr,θ方向に関する依存性を考慮しています．
論文番号 ２ 著者名 A. Samir, X. Yu and M. Isobe 論文題目 Optimal Dispersivity of Nonlinear Waves 討論者 質疑 Is there any physical meaning for the dispersivity index ? 回答 For regular linear waves propagateing over a uniform depth, the dispersivity error for any water wave model can be defined as the difference between the exact wavelength (or wave number) and the model predicted wavelength (or wave number) divided by the exact wave length (or wave number). For irregular waves, the dispersivity index is a squared value of the average dispersivity error for wave components weighted by the dimensionless energy associated with every component.
論文番号 ３ 著者名 大山 巧，土田 充 論文題目 非線形不規則波を対象とした自由波制御型の造波理論 討論者 池野正明（電力中央研究所） 質疑 １） このタイプの造波装置では，なぜ１次オーダーの造波板変位によって生じる自由波が発生しないのか？２） 通常，不規則波水路では１次オーダー成分を１００〜２００成分合成するが，この程度の成分数に対して，２次オーダーの和と差の周波数成分を実際に計算することが可能か？ 回答 １） 本形式の造波装置では，ピストンを十分に細い管路中に設けていますので，管路の断面積が変化しない場合には，流速が（流れ方向に）空間的に変化せず，流速を与える境界を管路中のどの位置にとってもよいことになります．すなわち，自由表面に接している通常のピストン型造波装置とは異なり（この場合は流速が空間的に変化する），造波板の有限振幅性に対応した自由波は発生しません．なお，水路底部での開口部とピストン設置位置での面積が異なる場合には，その断面積比を用いて流量補正すればよいことになります（海岸工学論文集 第４４巻，pp.11-15，1997参照）． ２） 本検討例では５０成分としていますが，自由波制御のための造波信号計算に要した計算時間はパソコンで数十分程度でしたので，成分数が１００〜２００となっても実用上の問題はほとんどないと思います．
論文番号 ４ 著者名 K. Nadaoka and K. Raveenthiran 論文題目 Development of a Phase-averaged Boussinesq Model and Its Application to Simulation of Long Wave Evolution 討論者 H. Kyotoh, University of Tsukuba 質疑 (Q1). The difference in orders of the long and carrier wave components between the present model and Schroinger equations. 回答 In the present model, it is assumed that the long wave (h, u) and carrier wave amplitude (A, U) components may become in the same order. But to derive the Schroinger type equations, which govern the coupled slow evolution of first-order amplitude A and mean flow potential f10, perturbation expansions and higher harmonics terms were assumed for (h, f) (Mei, 1983). In the corresponding solutions of the boundary value problems, the first order long wave component (h10) becomes zero and the remaining (h, f) terms are given in terms of first-order mean flow potential (f10) and first-order amplitude (A) . I.e. the Schroinger type equations are expressed in terms of first-order quantities. But the Schrodinger equations have a significant point that third-order nonlinearity affects first-order amplitude. The present model has nonlinearity in second-order because it was derived from a second-order improved Boussinesq equations. When a higher-order nonlinear phase-resolving model is used as governing equations, a higher-order phase-averaged model (such as similar to Schroinger equations) may be derived. This type of work will be reported in future. 質疑 (Q2). The effect of higher harmonic components in the present model. 回答 In the present study, only the first-order-zeroth (mean flow/long wave) & -first (primary/carrier wave) harmonic components are considered and the derived model is in second-order because which is derived from a second-order improved Boussinesq equations. According to the simulation results, the long wave comparisons (Figs. 1(b) and 2(b)) for both uniform depth and mild-slope bottom topography show clearly that the present model performs quite well. I.e. the long wave is mainly carried by the primary wave components and the effects from the higher harmonic components are negligible here. In carrier wave comparisons (Figs. 1(a) and 2(a)), the overall model predictions give confidence for the model but some discrepancies in shallow region in mild-slope bottom topography case suggest that the carrier wave expressions (equations (5) and (8)) are not enough to handle the highly nonlinear effect in shallow water regions. In this case, by incorporating higher harmonic terms to handle the nonlinear wave interaction, the present model may improved further. This type of work will be reported in future.
論文番号 ８ 著者名 手賀夕紀子，小林信久，多田彰秀 論文題目 不規則波と流れの干渉による波動場の変化 討論者 間瀬 肇（京大防災研） 質疑 1. wave blockageの条件に用いる波速Coはどの周波数を用いるのか． 回答 どの周波数を用いるか，一義的に決定するのは難しいので，ここでは便宜的にスペクトルピーク周期に対する波速Coを用いました．蛇足ですが，本論でwave blockageの条件に近い値を持つ場合のスペクトルは，スペクトルピーク周期に対応する周波数付近（約１Hz）でかなりエネルギーの減少が見られますが，もう一方のwave blockageの条件の値が小さい方のスペクトルは１Hz付近のエネルギーの減少がそれほど顕著ではないのが図−５からお分り頂けると思います． 質疑 2. エネルギーが遡れない場合のエネルギー平衡条件は，分散関係において波が存在し得ない周波数成分に対するエネルギー平衡条件も表わせるか． 回答 本論では，分散関係が求まる範囲のスペクトルについて，エネルギー平衡条件を適用しており，分散関係が存在し得ない周波数成分については現在のところ考察しておりませんので，実際のところよく分っておりません．今後，逆流による高周波領域における小規模な砕波ならびに表面張力波の発生について解析を進める場合に，このことについても検討したいと思います． 質疑 3. エネルギーを伝播できない，および波が存在し得ない条件においてはエネルギーが存在しないというフィルタリングが起こらないか． 回答 波が存在し得ない周波数成分でも，多少のエネルギーのLeakageが見られるようです．原因はよくわかりませんが表面張力と関係があるかもしれません． 質疑 4. 流れが場所的に大きくなっているところでは，高周波数領域においてエネルギーがフィルターアウトされるか． 回答 フィルターアウトの傾向は測定したスペクトル（図−５）に現れていますが，エネルギーのleakageも起っていると思われます．
論文番号 ９ 著者名 筒井 茂明・大木 洋典 論文題目 スロープおよびステップ型リーフ上での波の非線形挙動 討論者 合田 良実（横浜国大） 質疑(1) 図ー３に示されたマトリックスの各要素{Km}lにおける分散関係はどのようになっているのか教えて下さい．また，{K1}2，{K1}3などはストークス波の拘束波に相当すると思われるがいかがか． 回答 各要素においては，p.41の式(1)-(4)に示されているように，線形波の分散関係および群速度の関係が用いられている．すなわち，２，３，．．．倍周波数成分に対してはそれぞれの周期に応じた線形分散式と群速度が採用される．したがって，ストークス波理論の高次成分波の分散式にみられるような線形分散式の補正項の形とは異なります．また，マトリックスにおいて対角項{K1}2，{K1}3はモデル方程式(6)の左辺の線形項より得られる．これらは，質疑(2)の回答においても述べるように，基本周波数成分の自己相互作用あるいは基本周波数成分と倍周波数成分の相互作用などにより生じる高調波であり，その数理特性はご指摘の通りであると考えます． 質疑(2) 本論文集pp.46-50および第44回pp.6-10の拙論に示すように，非線形挙動を示すフーリエ高調波成分は拘束波と自由波の２種類で構成されているのが特徴であり，それぞれの振幅は一定である．貴論文，図ー４，５に見られるフーリエ振幅の場所的変化は波数の異なる同一周波数成分の線形重ねあわせによって生じる見かけの現象であり，成分波間にエネルギー授受があるとするのは誤りである． 回答 本研究で用いたモデル方程式(6)は，各成分波の非線形相互作用に伴う振幅の場所的変化を表している．その変化を.....(1)として，n=1なる基本周波数成分に着目すると，式(6)右辺の非線形項より，などに基づき変化することが判る．したがって，共鳴条件が成立する場合には，各成分波間に相互作用が生じて，振幅が場所的に変化する．また，n=2に対しては，なる自己相互作用より，高調波が生じることになる． 質疑では線形重ねあわせによって生じる見かけの現象であるとのことですが，上式(1)の，が一定となるように位相が与えられる場合に限り，ご指摘の通りであると考えます．しかし，式(6)を直接的に解釈する場合や一般的に水深変化がある場合には，成分波間にエネルギー授受があると考えた方が良いと思われます．もとより，非線形現象に関する理解は十分とは言い難く，今後とも研鑽したいと思います． 質疑(3) フーリエ振幅の再起間隔はで与えられます．ただし，k2は２倍周波数に対する自由波の波数，k1は基本周波数に対する非線形性を考慮した波数である． 回答 重要な事項に対するご教示，感謝致します．
論文番号 １３ 著者名 由比政年，石田 啓，保智正和 論文題目 界面の大変形を伴う気液二相流体場の数値解析 討論者 角野昇八（大阪市立大学） 質疑 図−６（表面張力が小さい場合の解析結果），および図−７（表面張力が大きい場合の解析結果）は，それぞれ，実現象でどのような条件に相当するのか． 回答 表面張力が小さい場合が,半径10cmオーダーあるいはそれ以上の気泡，表面張力の大きい場合が,半径1cmオーダーあるいはそれ以下の気泡を想定しています．
論文番号 １６ 著者名 二瓶泰雄、灘岡和夫 論文題目 移動境界追跡型混相乱流計算手法の開発 討論者 重松高昌（大阪市立大） 質疑 本モデルでは、気泡の取り扱いは比重の軽い固体粒子と同等か？ 回答 ここでの気泡粒子の取り扱いは、球形で径一定としていることから、ご指摘の通り、比重の軽い固体粒子と同等な取り扱いとなっている。
論文番号 １７ 著者名 山下隆男 論文題目 砕波帯近傍における海面せん断応力の評価法 討論者 加藤 始（茨城大学） 質疑（１） 図-2(a)は風速変動に慣性小領域が存在することを示すものとしては不十分ではないか？通常は-5/3乗の上下は高周波側できつい勾配，低周波側で緩やかな勾配になる。 論文でf>2Hzでは慣性小領域に入らないと書かれているのはどのような理由からですか？データのΔtが大きすぎて計算スペクトルのfmax以上にパワーが残っているということではないでしょうか？ 回答 図-2(a)は風速変動に慣性小領域が存在することを示すものとしては不十分であると認めます。実際にはスペクトルが-5/3乗の領域（慣性小領域）に入っているケースがかなりあります。論文中に載せた例は，解析に用いたケースを無作為に１例取り出してきたものです。海からの風の場合にはスペクトル形状から慣性小領域にあると思われるケースは多く認められます。 風速は超音波風速計で計測しております。サンプリング周波数は10Hz，風速計自信の分解能もこの程度と表示されています。風速に依存しますが，離散化データとして使えるのは５Hz程度以下だと思って使用しております。米国での報告ですが，パワースペクトルが慣性小領域にあるのは，大気の安定度の高い場合で，風速10m/sの地上10m地点でのデータでは2Hz以下であることが観測されていますので，ここでは風速計自身の分解能とこのことを考慮して２Hz以上は解析の対象としませんでした。もし，高周波側も対象とますと，抵抗係数CDはさらに大きくなります。一方，低周波側がどこまで慣性小領域にあるかということが大きな問題で，今回は２Hz〜0.6Hzの間でせん断応力を見積もりました。これも大気の安定度と関連しますが，この間では慣性小領域にあると思われるケースが多かったので，どのケースもこの間で計算しています。 質疑（２） 図-４のU10=20m/s付近でCD=0.003という値も外洋における値よりやや大きいが，U10=10m/s付近でCD=0.01というのは外洋での値CD=0.001に比べて１桁大きいがどうしてでしょうか？ 回答 求めた抵抗係数が大きいこと，風速依存関係が従来外洋で計測されたものと逆で，風速が高くなると抵抗係数が減少し，外洋での値に近づく結果となりました。風速10m/sでは従来の値より１桁大きくなっています。これには以下のような問題があると思っています。 （１）低風速になると慣性小領域から外れるケースがあるが，解析の対象としたデータにもこのようなケースが含まれている。すなわち，TDMの適用領域外にある。 （２）低風速になると，データはTDMの適用領域内であっても，風速計プローブの支柱，観測桟橋自身によって発生する乱れの影響が相対的に強くなり抵抗係数が大きくなっていることが考えられます。 また，抵抗係数が大きくなっている理由の一つには沿岸部での波浪の粗度としての要素が大きくなる（波形勾配がきつくなる）ことも考えられますが，外洋のそれと比べて１桁大きいのは，これ以外にも風速計プローブの支柱，観測桟橋自身からの乱れの生成効果が入っていると思っています。
論文番号 １９ 著者名 ムスタファ アタウス サマド・田中 仁 論文題目 不規則波動下の底面せん断力特性に関する研究 討論者 浅野敏之（鹿児島大学） 質疑 In the paper, k-e model was used to judging accuracy of the proposed models. But I do not think k-e model provide 100% accuracy because it is originally proposed for unidirectional flows without laminar and turbulent transition. How do you consider on that? 回答 Although k-e model was originally proposed for turbulent computation in unidirectional flows, over the years it has also been used extensively to compute flows with different pressure gradient conditions. With gradual availability of experimental and direct numerical simulation data on oscillatory boundary layer flows, many researchers have successfully applied k-e models to simulate turbulent flows, mainly for sinusoidal wave conditions. The leading works came from Jensen et al.(1989) on experimental aspects and from Justesen and Spalart (1990) on k-e model computation. Sana and Tanaka (1996), and Sana (1997) have tested the applicability of different available k-e and k-e models and compared the results with experimental and Spalart and Baldwin (1996) DNS data covering a wide range of Reynolds numbers for laminar, transitional and turbulent flow regimes. It has been concluded that among the six models tested for oscillatory flows, Jones and Launder original low Reynolds number k-e model provided best predictive ability for sinusoidal cases considered. It is argued that, considering turbulent time scales, the flow over most of the domain is quasi-steady, and the perturbation originate at the bottom and diffuse in the upward direction. Therefore, close to the bottom improvements those could be achieved by employing models of more complex nature might not be very significant. This is also evident when the computation of Hanjalic et al. (1993) with Reynolds stress model is compared with experimental data. Therefore, in light of the finding from previous researchers, it could be concluded that although it would not be possible to achieve 100% accuracy in turbulent computation using k-e models for oscillatory flows, however, the level of accuracy that is generally achieved would be of much practical value. Ref.: Jensen, B.L., Sumer, B.M. and Fredsoe, J., 1989, Turbulent oscillatory boundary leyers at high Reynolds numbers. J. Fluid Mech., 206:265-297 Justesen, P. and Spalart, P.R., 1990, Two-equation turbulence modelling of oscillatory boundary layers. In: Proc. 28th Aerospace Science Meeting, Reno, Nevada, USA, pp.1-9 Sana, A. and Tanaka, H., 1996, The testing of low Reynolds number k-? models by DNS data for an oscillatory boundary layer. In: Flow Modeling and Turbulence Measurement VI, pp.363-370 Sana, A., 1997, Experimental and numerical study on turbulent oscillatory bottom boundary layers. Ph.D. Dissertation, Department of Civil Engineering, Tohoku University, pp.174 Spalart, P.R. and Baldwin, B.S., 1989, Direct simulation of a turbulent oscillatory turbulent boundary layer, In: Turbulent Shear Flows 6, Springer-Verlag, pp.417-440 Hanjialic, K., Jakirlic, S. and Hadzic, I., 1993, Computation of oscillating turbulent flows at transitional Re-Numbers. In: Turbulent Shear Flows 9, Springer-Verlag, pp.323-342
論文番号 ２２ 著者名 平山秀夫 論文題目 砕波帯内における戻り流れの鉛直分布の理論とその再検討 討論者 安田孝志（岐阜大学 土木工学科） 質疑 砕波帯内にあっても波動モードが卓越し，進行波の質量輸送モデルで戻り流れが説明できると考えてよいのでしょうか． 回答 砕波帯内では，砕破に伴う大規模水平渦の生成・発達・移流拡散，あるいは斜降渦の生成やそれに起因するスパイク状の鉛直流の発生等，３次元性を帯びた複雑な乱流運動場である．特に水表面付近では，砕波によって発生する多量のmass fluxによって強いせん断流が生じ，その補償流として戻り流れ(undertow or return flow)が発生し，これが底質移動の要因の１つであることは周知のことである．一方，砕波帯内では，このような渦運動への波動エネルギーの遷移によって波動成分は著しく減衰するものの，波動運動はまだ依然として残存しており，砕波帯内の流体運動を支配していることは，これまでの実験的事実から明らかである．従って，砕波帯内の波動成分は，水表面付近の強い渦・乱れ・流れの影響で，波数等その特性が変化することはあっても，進行波成分は本質的に維持されているものと考えられるので，著者は砕波帯内における戻り流れも基本的には進行波モードで説明できるものと考えている．このことは，Longuet-Higgins(1953)のconduction equationでも的確な水面渦度の推定値を与えることさえ出来れば，砕波帯内の戻り流れの鉛直分布をかなりよく説明できることからも明らかである．
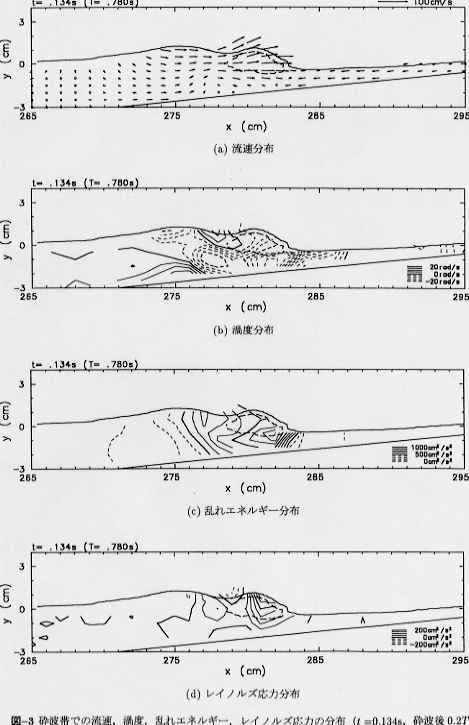
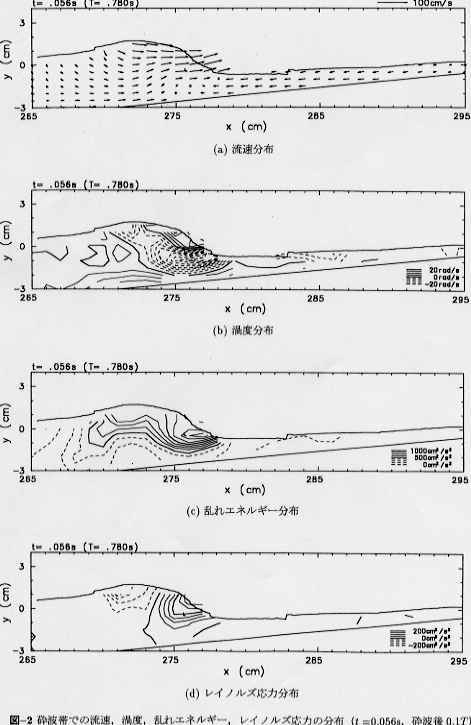
論文番号 ２３ 著者名 宮本恭交・長尾昌朋・新井信一・上岡光男 論文題目 周期波の砕波帯での可視化手法を用いた乱流計測 訂正 図−２，図−３を発表で使用した50周期分の位相平均を施したものに変更．
討論者 岡安章夫（横浜国大）
質疑
乱れエネルギーとレイノルズ応力を算出する際に，位相平均流速を求める時に取り除いた異常な流速値はどのように考慮しているのか．異常値として判断されたものが真値である可能性はないのか．
回答
位相平均流速分布を算出する際，着目する点から半径1cmの空間を設定し，その中に存在する実測流速から局所的な流速分布を算出しています．この空間は時間方向へも及ぶため，トレーサ粒子が波速程度の70cm/sで移動しているとすると，この空間を横切る時間は最大0.0028sです．1/400s毎に撮影された可視化画像から流速を算出しているため，1個のトレーサ粒子からは10個程度の実測流速が位相平均操作に使用されることになります．よって，連続して得られた実測流速の全てが誤りである可能性は非常に小さいこと，位相平均空間には複数個のトレーサ粒子が存在すること，50波程度の波で位相平均したことなどを考慮すると，平均値からのずれが標準偏差の2倍以上を異常値とした場合，異常値の中に真値が含まれる可能性は非常に小さいと考えられます．
このようにして取り除いた流速は，その大きさや方向が乱れとしても考えられないほど異常であるため，乱れエネルギーやレイノルズ応力の算出にも用いておりません．
質疑
特性値の分布を見ると，一般的に気泡混入領域において高い数値を示しているが，相関法と追跡法の手法の違いが分布に影響しているとは考えられないか．
回答
気泡混入領域ではトレーサ粒子の識別が不可能であるため，この領域での流速測定にはは相関法のみを使用しております．可視化画像から流速を推定する場合，トレーサ追跡法では1個のトレーサ粒子から時系列データを取得しますが，相関法では測定点を固定するため毎回異なったトレーサを使用していることになります．このため，前出の質疑回答の内容を考慮すると，異常な流速値が十分に取り除かれない確率が上昇すると考えられます．また，砕波帯のように流体の変形量が大きくなると，相関法で得られる流速の精度は低下してくると考えられます．このようなことから，気泡混入領域とその他の領域では，流速測定の精度が若干異なると思われます．しかし，乱れ強度が流速の50%程度であることを考えると，絶対値にやや誤差が含まれるものの，ほぼ妥当な分布ではないかと考えられます．今後，より精度を高めるため，可視化画像の撮影法や誤流速の除去法を工夫したいと思います．
討論者 斎藤武久（金沢大・工学部）
質疑
水表面の変動をともなう場合（その内でも砕波時のようにジェットを含む複雑な水面形の場合は特に），レーザーシートを照射した際，水表面における光の散乱や反射の時間変化によって，レーザーシート光自体にむらができ，得られる画像データの輝度分布が正確にとらえられなくなるおそれはないでしょうか．もし，あるとすればその対応策について教えていただけないでしょうか．
回答
可視化画像の輝度むらは流速の推定精度へ影響を与えますが，流体の状況，画像の撮影法，流速の推定法などによって対策が異なります．よって，今回の実験での対策を中心に返答いたします．
砕波直前までの大きな問題点は水面の変形によるレーザーシート光の輝度の揺らぎです．これは，底面からレーザーシート光を照射することで対応できますが，レーザーシート光自体の輝度むらは考慮しなければなりません．しかし，底面から照射することで輝度むらが時間的に変化しないため，あらかじめ輝度むらを測定し，2値化のためのしきい値に分布を持たせる，可視化画像の輝度を補正するなどの方法で対応します．
砕波後の気泡混入領域ではトレーサ粒子の識別は困難であるため，この領域では相関法のみを使用しています．相関法はテンプレート内の輝度パターンを次の画像の輝度パターンと比較するのですが，原理上テンプレート内の輝度の平均値は考慮していないこと，テンプレートの大きさを輝度むらの大きさより小さくすること，画像間の時間間隔を輝度むらが変化する時間より短くすることなどに注意すれば，輝度むらがあってもそれほど流速推定精度は低下しないと考えられます．ただし，上述のレーザーシート光自体の輝度むらや水面や底面の写り込みには対策が必要だと思います．
論文番号 ２５ 著者名 渡部靖憲，梅田克史，佐伯浩 論文題目 砕波後のレイノルズストレス及び乱れエネルギー変化の特性 討論者 安田孝志（岐阜大学） 質疑 計算結果と自由度の関係はどうなっているのでしょうか？ 回答 乱流を評価するためには３次元流速場を取り扱う必要があるという意味の質疑ととらえまして回答します．やはり，自由度が少ない分乱れ評価が不適当になり，特にボア領域において２次元と３次元との相違が大きくなるのだろうと考えています．レイノルズストレス輸送方程式による乱れの発達の考え方から言えば，初めはu'u',w'w'の２つの方向の乱れ成分が発生し，これらの成分は乱れエネルギーとして次に３方向に再分配されます．分配されたエネルギーはu'w'等のレイノルズストレスの生成に寄与します．２次元計算の場合は分配される自由度が少ないため各方向成分の乱れエネルギーが不適当になり，結果として平均流速場へも影響を及ぼすと考えられます．ただし，定量的にどれほど影響があるかは，まだ比較できておりません．今後，当然行わなければならない比較であると考えていますが，計算機の問題から，２次元計算と同一のグリッド幅を持つ座標系で計算を行うことは現在不可能であり，別のテストが必要と考えています．
論文番号 ２８ 著者名 渡部靖憲，松本靖治，佐伯浩 論文題目 砕波帯内の３次元的水粒子軌道の実験的研究 討論者 岡安章夫（横浜国立大学） 質疑 論文中図-12に対して「方向性を持たない発達した速度場」というのは「３次元性の等方性の乱れ場」と解釈して良いのか． 回答 今回の実験では，計測機械の都合からフレーム間隔1/30秒のビデオカメラを使用しました．一般的には，この時間間隔の振動成分をもって乱流域の運動と称することはできません．本研究は，大規模渦によるラグランジュ的水粒子を追跡することを目的とし，小スケールの乱れについての議論は困難ですが，遷移領域を通した図-10，図-11，図-12中の明確な運動形態の相違は，少なくても水平渦等の顕著に方向性を持った大規模渦が拡散あるいは分解され，３次元的に振動する異なる性質をもつ渦に遷移した結果であると解釈しています．等方性に関する議論は，時間間隔及び粒子径をさらに小さくして実験を行う必要があると思います．
論文番号 ２９ 著者名 有川太郎・磯部雅彦 論文題目 非線形緩勾配方程式を用いた砕波モデルの確率 討論者 合田良美 質疑 砕波のメカニズムを細かく取り込んで，数値計算法を改良されている努力は多とするが，最終目標がやや不明瞭である．ヨーロッパ，カナダのBoussinesq方程式方式に対抗し，それを「凌駕」するだけの学術的・実用的に優れたモデルの完成を目指していただきたい．そのためには，複数のボトルネック個所の重要度を比較勘案し，なにを最初に解決すべきかをまず考えることが必要である． 回答 最終的な目標は，複雑な波浪場でも精度のよい計算を可能にするための数値モデルを開発することです． Boussinesq方程式と非線型緩勾配方程式を比較した場合，確かにBoussinesq方程式も高次の分散項を加えることにより，広範囲の計算が可能となりますが，そのための数値計算テクニックが難しくなります．それに比べ，非線形緩勾配方程式は，任意の分散項を取り込め，数値計算的にも取り扱いやすくなるという利点があります．そこで，非線形緩勾配方程式と等価な砕波モデルを構築しようと考えました． これまでの砕波モデルの多くは，進行性の砕波の再現に着目しています．それでは，重複波などの砕波の再現に直接適用するのは理論的ではありません．そこで，砕波そのもののメカニズムを取り込むことにより，いろいろな砕波に適用できるように考えたのが今回のモデル化につながりました． 最終目標は上述しましたように，様々な波浪場の予測を可能にすることです．そのために砕波をまず表現できるようにし，そうすることで，流れの予測も可能になると考えています． 今後は沖側から流れや波浪が与えられるだけで沿岸での波浪や流れの予測を可能にしたいと考えています． 以上です．たくさんの人に使っていただけるモデルにできるよう，今後も努力します．
論文番号 ３０ 著者名 渡部靖憲，森憲広，佐伯浩 論文題目 砕波の３次元Large Eddy Simulation 討論者 岡安章夫（横浜国立大学） 質疑 第２波のジェットの突っ込みで，先端部が沿岸方向に不均一になるのは，第１波による組織渦の影響か．また，逆にジェットの不均一が組織渦の生成に大きく関与していると考えられるか． 回答 着水までほぼ２次元的であった第１波の砕波で生成された渦は，第２波のクレスト前面の沖向きの波動による流速及び第１波の進行で誘発された戻り流れにより沖向きに移流され，さらに砕波点近傍の強い上向き流速に移流されジェット近傍にまで達していました．明らかにジェットの水面形はこれらの渦に影響を受けていると考えられます．これに関しては現在さらに詳細に調べております．また，今回は第２波の砕波直前までしか報告できておりません．この水面の不均一さがどのように渦生成に寄与するか現在調べております． 討論者 趙群 （埼玉大学） 質疑 Reynolds数定義 回答 Re=Ch/n (C;波速，h;造波境界における水深，n；動粘性係数）です． 質疑 なぜガウシアンフィルターの採用？ 回答 フィルターの選択に関しては，最もポピュラーであること以外特に大きな根拠はありません．
論文番号 ３１ 著者名 趙群、 谷本勝利、中村広昭 論文題 LES−VOF法によるリーフ上での数値波動解析 討論者 M．A．Hamzah 質疑 １） Have you ever compare the calculation results for the case with or without turbulence term? ２） Did you compare your result with k-e model? 回答 １） Our results showed that the turbulence terms have some effects on the surf zone dynamics: the velocity form and the position of breaking point. ２） We have not compared our results with the one from k-e model yet.
論文番号 ３４ 著者名 吉田 茂，早川典生，細山田得三 論文題目 透過性潜堤内外の流れ構造について 討論者 合田良実（横浜国大） 質疑 対象とする構造物である潜堤は海岸保全が主目的であり，波高伝達率やエネルギ−減衰率を解明することが研究の最大の目標と考えられる。その意味で不透過の場合との比較計算を通じて潜堤内部の透過性の役割を理解し，潜堤の波浪減殺効果をさらに高める方策を工夫することが望まれる。早く計算法を発展させ，実際構造物の機能解明を行うべきである。 回答 本研究では実際の海岸で用いられている潜堤で問題となっている潜堤の法先や法尻での侵食，潜堤背後での洗掘に対して，入射してくる波の流速や渦がどの程度関わっているかを調べることを目的とした基礎的な研究である。 最終的には数値計算的な手法によって解決することを視野にいれており，計算手法を検討するに際して，比較のために必要な流れ場全体の流速ベクトルや渦について出来るだけ精密にとらえるための実験を行った。 一方数値計算として，ここではＳＯＬＡ−ＳＵＲＦ法の適用の可能性について示した。 御指摘のあったものは重要な事柄であり，これらについても現在，研究を進めている。
論文番号 ３５ 著者名 内田一祐，服部昌太郎 論文題目 波打ち帯波動場と底面せん断力特性に関する実験的研究 討論者 出口一郎(大阪大学，土木) 質疑 １． 流速最大値と最大せん断力とを関係つけたときの，摩擦係数ｆの値はどの程度であるか． ２． 滑面・粗面にかかわらず，実験は不透過斜面で行われている．通常粗度が大きくなると，底面の透過性も増加する．具体的には，どのような状況を想定して実験を行ったか． 回答 １． 流速とせん断力間の位相差が考慮されないため，打上げ帯内での摩擦係数に系統的な傾向 は認められない．しかし，本実験ではｆ＝0.06〜0.8の値をえている． ２． 捨石マウンドのような透水性を持つ斜面では，打上げ時では浸透，打下げ時ではその自由流出の効果を考慮する必要がある．表面粗度と浸透性とは密接な関係があるが，これを適切に表現する関係がないことと，規則波が砂海浜の波打ち帯に打上げる場合には，砂海浜での浸透効果が小さいことを想定して，実験を行った． 討論者 真野 明 (東北大学，土木) 質疑 実験領域が層流域なので，底面粗度をつけてもその効果はないのではないか． 回答 静水汀線より岸側では，ご指摘の通り粗度の効果がありません．しかし，静水汀線から沖側では水深も大きく，また砕波あるいはturbulent boreがもたらす影響で，波動場は乱流域となり，汀線での入射波特性とwave setupに変化が見られます．この状況を考慮して，斜面粗度は砕波点沖側から岸側に施設した．
論文番号 ３６ 著者名 M.A. Hamzah，間瀬 肇，高山知司 論文題目 孤立波の遡上と海岸堤防への波力に関するダイレクト・シミュレーション 討論者 真野 明（東北大学） 質疑 乱流モデルを用いないで直接ナビア・ストークス方程式を計算する場合必要なメッ シュサイズが小さくなりすぎるのではないか． 回答 ここで用いた計算法は可変メッシュサイズを用いており，放物線的に汀線付近を細 かくしている．すべてを細かくすると計算が大変になるからである． また，粘性係数は実際の水のそれではなく，Lemos (1992) によって用いられた値 を用いている．
論文番号 ３７ 著者名 後藤仁志・酒井哲郎・沖 和哉・芝原知樹 論文題目 粒子法による巻き波型砕波を伴う斜面遡上過程の数値シミュレーション 討論者 二瓶康雄（東京工業大学） 質疑 自由表面での力学的境界条件として，表面張力の効果をここでは取り込んでいないが，その点に関してはどのように考えるか． 回答 重要な指摘かと思います．ある種の粒子間引力を水表面粒子間に作用させるといった方法で対応できるのではと考えますが，今後検討したいと思います． 討論者 濱田純次（竹中工務店技術研究所） 質疑 表面の粒子は圧力をゼロとおいているが，この粒子の圧力勾配を計算する場合，(4)式のn0はその粒子のnを用いるべきだと思いますが，どのようにしていますか． 回答 n0は一種の基準値で，計算の初めから最後までは変化しません． 質疑 (3)による圧力は仮の圧力と思われますが，粒子法で波力や流体内部の圧力は精度よく計算できますか． 回答 粒子法では，接近しようとする粒子を跳ね返す駆動力として圧力が効いているので，圧力の微少変動は不可避です．ある種のスムージングである程度対応できる見通しは持っておりますが，現時点では明確に回答できません．今後検討したいと思います．
論文番号 ３９ 著者名 加藤 茂・山下隆男・安田孝志・三島豊秋 論文題目 高次乱流モデルとローラー型砕波モデルとを援用した海浜流の３次元数値解析 討論者 日野幹雄（中央大学） 質疑 １．平均流の基礎方程式にradiation stress termが落ちている．これがないとwave-setup，-setdownや沿岸流系の現象が出ない． ２．沿岸域のような比較的スケールの小さい所で，Mellor-Yamada乱流モデルは適用可能なのか？Mellor- Yamadaのモデルは，ほとんどメソスケールに適用されてきた．LESやk-εとの比較を行い，各モデルの適用度の検討が必要と思うが． 回答 １．本研究で用いている平均流モデルは，流速をu=u+u'(u：平均流速，u'：平均流速からの変動成分）と仮定して導いています．したがって，uをさらにu=U+uwave（U：平均流速，uwave：波動成分）と仮定すると，radiation stressに相当する項が表れます．本研究では長期かつ広域的な海浜変形観点から海浜流の主要因になると考えられる風によって生成される吹送流などの（時間・空間の両方において）比較的大規模な流れと波浪による流れを併せて平均流として扱っているために，radiation stressに相当する項（波浪の影響）は平均流モデルに陽的には表れていません．よって，ご指摘の通りwave-setup，setdownは表現せれません．しかし，波浪の流れに及ぼす影響としては，波浪（砕波）モデルにより求められる砕波による海面せん断応力が海面での境界条件に考慮されるため，波浪による流れの生成も考慮され，波高分布と海底地形に伴った海浜流場も形成されます．今後，数値計算結果および観測データとの比較からradiation stressと砕波による海面せん断応力項の対応，砕波による海面せん断応力項の適用性について検討していきたいと考えています． ２．LESやk-εとの比較も必要であると思いますが，特にk-εモデルは用いられている係数（定数）が実験結果に基づいて決定されているものであり，それをそのまま現地に用いることの方が問題であると思われます．用いられている係数に関する問題については，本研究で用いているMellor-Yamadaの乱流モデルにおいても言えることであり，今後，現地観測データとの比較から，乱流モデル内で用いられてる係数の検討を行い，Mellor-Yamadaの乱流モデルの沿岸域，特に砕波帯内での適用について考えていきたいと思います．
論文番号 ４１ 著者名 山下隆男 論文題目 ADCPにより長期連続観測した海浜流の鉛直分布とその強風，波浪応答特性 討論者 日野幹雄（中央大学） 質疑 離岸流は沿岸沿いの特定の場所から比較的狭い幅で発生する。この実測できれいに離岸流が捉えられているのは，偶然離岸流の発生する地点であったということか？ 回答 そうです。大潟波浪観測所の観測桟橋はこれまでにも離岸流の発生する地点に位置していることはわかっていました。今回の観測では離岸流の発生する波浪，風条件を知ることができました。離岸流は常時発生しているのではなく，以下のような場合に発生します。 （１）ストームの終わりに風が弱まり，風向が変化した場合に約６〜１２時間連続して発生します。 （２）汀線に直角方向の強風，高波浪が長い期間（１日程度）連続して作用した場合には，波浪，風条件の顕著な変化が無くても発生します。この場合には離岸流発生期間が長くなります。 （３）多くの場合，（１）のタイプですが，1998年の冬期の連続観測では，約１０回発生した離岸流の内，（２）のタイプが２ケースだけ観測されました。
論文番号 ４２ 著者名 泉宮尊司・斎藤雅弘 論文題目 極値統計解析における不偏性条件式ならびに漸近理論による信頼区間の推定 訂正 式(18)において, =An] は不要で削除する。 式(26)の３行目の giyR+hj を gj y R + hjに修正。 式(30)の３行目： [ξi,ξj][ξi,ξj]を[ξj−ξi] [1-ξj]に訂正。 式(32)の２行目： piをpjに, ４行目：piをpjに訂正。 式(34)：lnψ(xi,xj)をlnψ(zi,zj)に訂正, （xj-zi）を(zj-zi)に訂正。 討論者 合田良実（横浜国立大学） 質疑 非常に綿密な理論的・数値的ご検討に敬服致します。積率法の適用に際しては, 標本分散の期待値が母分散より小さいことが知られていますが, この補正をどのようにされたのかお教え下さい。なお, Gumbelの与えたFT-I型分布に対する補正式は討論者のシミュレーション結果によれば不正確です。 回答 著者らの論文に興味を示して戴き, 有難うございます。ご質問の標本分散の件ですが, 式(17)で与えられるs2 は不偏推定量ですが, 平方根をとったsに関しましては不偏推定量ではないことが知られています。従いまして, 本研究ではs2 に関して先に期待値をとって標本の分散を評価しております。このようにすることによって, バイアスがない推定を行うことができます。漸近理論値に関しては, 同様な操作を行うことによって真の母分散に等しくなることから, 真の尺度母数を与えて計算しております。積率法では, R年確率統計量が式(22)で与えられることから, sの負のバイアスのため, xRも負のバイアスが生じることになります。この差異は, 漸近理論によって計算することができますが, Г関数を用いて表すことができます(参考文献(１)の374p.)。N=10のとき, E(s)=0.9727σ, N=20のとき, E(s)=0.9869σ, N=30のとき, E(s)=0.9914σ, N=50のとき, E(s)=0.995σとなります。この結果は, 討議者が行った対数正規分布やワイブル分布のk=2の結果（参考文献(２)の54p.）とほとんど一致しています。これは, これらの分布が正規分布に近いため, 漸近正規性が速く現われるためと考えられます。 なお, 部分極値資料に関しましては, 母分散の推定に式(17)を用いるよりも推定された尺度母数Aから理論式によって推定した方がよいと思われます。 参考文献 (1)中山伊知郎編(1968)：統計学辞典 増補版, 東洋経済新報社, 374p. (2)合田良実(1988)：極値統計におけるプロッテイング公式ならびに推定値の信頼区間に関する数値的検討，港湾技術研究所報告, 第27巻, 第１号, 54p.
論文番号 ４５ 著者名 北野利一・間瀬肇・中野晋 論文題目 浅海不規則波浪の周期の統計特性 討論者 合田良実（横浜国大） 質議 (1) 図-２はH-Tの結合分布の表示法として分かりやすい． 図-６で false wave がH-Tともに小さい波であることが示されているが，図-２のデータから false wave を除いたものでもやはりHとTがともに小さい部分が残るのではないだろうか？ 回答 ご指摘のように，false waveを除いたものでもやはり，HとTがともに小さい部分が残ります．これらの『原点を囲む周期が短く波高も小さい波』は，本質的に波として認識しておく必要のある波であると考えています．しかし，論文中にも述べているとおり，この小さな波を詳細に議論することは難しいため，ここでは，発生確率が高く，相対的に大きな波を対象に議論しています． 質議 (2) 式(7)で定義されるνが周波数スペクトルのモーメントから定義されるものに等しいことの根拠を提示して頂きたい． 回答 式(7)が線形不規則波の場合に成立することについて，式を用いた説明は，Gimenez et al. (1994)（論文の参考文献を参照）のAppendix A にあります．なお，線形不規則波の確率密度分布がη-ξ平面で点対称であるという観点から，式(7)の導出を試みているところです． コメント (1) “false”の発音は，ファルスではなく，フォールスです． 回答 御指摘ありがとうございます．イタリア風読みになっておりました． コメント (2) 式(1)を最小自乗法による理論と称するのは不適切です．拙著でしっかり勉強して下さい． 回答 御指摘のとおり，今回の論文中には“一種の最小自乗法による理論”との記述のみで，その確かな根拠が書き切れておらず，誤解を招く結果になっています．ここでは，少し式を用いて私の意見を整理させてもらいます． Longuet-Higgins の周期に関する理論（1975および1983）で用いられる確率分布の基礎式を誘導するために，まず，水位変動をある代表周期のまわりで展開して，以下のように変形する． ここで現れる以下に示す と，そして，その微係数 との４つの量を確率変数に選ぶ． これらの確率変数は中心極限定理より４元正規確率分布に従うことがわかり，具体的な分布関数を得るのにはそれぞれの共分散が必要となる．ここでは，特にの速度の変動を表す との分散に注目する． 上式で，代表周期を適切に選ばないと分散値が過大に評価されるため， となるを選べば最適であると考えらる．そして，その最適な代表周期は，スペクトルモーメントより定義されるスペクトルの重心，つまり，となる．また，このときの最小値をもとに帯域幅パラメータを定義し，その最小値をと表す．以上の考察から，本理論の基礎式が“一種の最小自乗法による理論”であると解釈しました． 以上の説明は，今回の論文作成時に，天下り的に平均周期で展開している原著から受けた印象でしたが，よく考えると，単なる個人的な一解釈（あるいは誤った解釈）であるような気もしてきました．平均周期で展開することが理論構成上のkeyとなる事柄であるのか否かについて，合田先生の著書をしっかり再読し，現在検討中です．新たな理論的事実が得られ次第，報告させていただきます．
論文番号 ４６ 著者名 太田隆夫，木村 晃 論文題目 ニューラルネットワークを用いた有義波高の予測について 討論者 間瀬 肇（京都大学，防災研究所） 質疑 因果関係を考慮してネットワークを同定した方が良いのではないか．波高の時系列を学習するだけでは，急な（突然の）気圧変化に伴うような波高予測ができない． 回答 当初は，比較的周期性のある日本海側の冬期波浪の変動パターンを，ニューラルネットワークで抽出できないかと考え,最も簡単な自己回帰的モデルを使ってみました．結果的にはそのようなパターンを抽出できたとは考えられず，やはり気象要素を取り込んだモデルを用いる必要があると思います．今後，気象データを用いたモデルについて検討したいと考えております．
論文番号 ４７ 著者名 安田孝志，大宮雄一，河合篤司，小林智尚 論文題目 非線形干渉による平面波の不規則化とその特性 討論者 横木裕宗（茨城大 広域水圏センター) 質疑 波高計アレイの配置（図-13)は，同じようなベクトルになるような配置になっているようであるが，どのようにしてこの配置を考えたのか． 回答 本数値計算で，ある固定点での水位の時系列データを取得するために定めました波高計のアレイの配置につきましては，実際の現地観測とも対応できますように，当初4台の波高計によるスターアレイとしておりました．しかし数値計算結果でありながら波浪の空間情報が少なすぎるという判断から，スターアレイを残した状態で新たな波高計を配置することとしました．しかしながら波高計を設置する場所は，規則的で離散的な数値計算のグリッド上に限定されるため，あまり自由度がありませんでした．ご指摘のとおり本来ならば波高計の組み合わせのベクトル距離は異なるように配置すべきですが，上記の理由から論文集に示しました配置となっております． ベクトル距離の重複による情報量の低下につきましては，波高計そのものの台数を増やすことにより十分補われていると判断しております．ただしベクトル距離の重複による情報の重複という問題につきましては解析結果に対する影響は検討しておりません．
論文番号 ４８ 著者名 泉宮尊司・二木 央・泉 正寿 論文題目 微積分方程式を用いた方向スペクトルの高精度推定法に関する研究 訂正 式(9)の２行目： iθ*をd θ*に訂正 討論者 横木裕宗 質疑 (1)波高計などの配置間隔と周波数帯の間隔によっては,方向分布関数の推定精度が異なると思うのですが, 推定された例があれば教えて下さい。 (2)入射波と反射波が混ざっている波浪場に適用するのは簡単なのでしょうか。 回答 (1)本研究では, 波長L=80mで計算を行っており, 設置間隔を変えた計算は行っておりません。当然のことながら, 相対間隔が変化すれば, 方向スペクトルの推定精度も変化すると思います。広い周波数帯に対して精度よく方向スペクトルを測定するためには, 種々の間隔と方向成分がどうしても必要となるために, 観測地点数を増やす必要があります。今回の計算では, １地点から４地点までの比較的数少ない観測法でシミュレーションしておりますので, これをもう少し増やして計算を行う必要があります。 (2)入射波と反射波が混入している場合にも, この計算法の拡張ができると思います。反射率を周波数と方向の関数として, 汎関数に取り入れることによって, 反射率に関する微積分方程式が得られます。 ただし, 反射率には0
論文番号 ６５ 著者名 土田 充、大山 巧、平石哲也、富田孝史 論文題目 港内係留船舶の長周期動揺に基づく静穏度評価法について 討論者 合田良実（横浜国大） 質疑 （１）ばね定数を変化させたときに船体動揺量とともにばね張力のスペクトル計算を行い、例えば1/100、1/1000超過値の頻度分布の計算結果も提示されるとさらに実用的と考えます。 （２）圧力勾配の絶対値と船体動揺量の関連付けを考慮した上で、圧力勾配についても特定周波数についてのみでなく、スペクトル計算による年間の超過確率の形でまとめていただきたい。 回答 （１）係留索断裂時に対応した限界ばね張力を適切に設定すれば、ご指摘の中にありました係留索断裂の頻度分布を算定することは、比較的簡単だと考えております。ただし、実際の荷役作業では、限界張力になる前に係留索を緩めて荷役作業を中断し、断裂を回避しているようです。本研究では、周波数領域で計算を行っているため、こういった係留索のオペレーションを考慮することはできません。したがって、この係留索断裂の頻度分布の算定法を現地に適用する際には、超過確率を係留索の断裂率ではなく、張力の観点からみた稼働率とすることが適切だと考えます。 （２）ご指摘の通りに圧力勾配振幅と船体動揺量を関連付けることで、限界圧力勾配振幅をどの程度にすべきかが明らかになり、圧力勾配振幅を簡易静穏度指標として採用するうえで非常に有意義であると考えます。 討論者 椹木 亨（大阪産業大学） 質疑 荷役機械の種類を荷役限界に入れるべきである 回答 対象とする船舶によって荷役機械の種別が異なるため、限界動揺量が異なることは承知しております。本研究では、限界動揺量の設定をUeda and Shiraishi（1988年の港湾技術研究所報告, 第27巻, 第4号, pp.3-62）に依拠しており、一般貨物船の限界動揺量を採用しております。
論文番号 ６６ 著者名 佐藤愼司，小杉俊夫，加藤憲一，口石孝幸 論文題目 西湘海岸における台風9720号による海岸災害とその原因 討論者 合田良実（横浜国大） 質疑 天文潮と高波が一致して災害を大きくしたことは分かりますが、9720号の規模・経路からみてこのように大きな被害を出したのが理解困難です。これ以前の台風災害と比べて今回の災害が大きくなった自然要因についての調査結果を補足して頂ければ幸いです。 回答 西湘海岸では、1979年と1982年の台風来襲時に、西湘バイパスの道路陥没等の海岸災害が発生しています。この時と比べて、今回の台風は以下のように波高が大きかったことが、まず原因の一つとしてとして挙げられます。ちなみに、1979年および1982年には、今回大きな被災を受けた御幸ヶ浜の大規模突堤はありませんでした。 1979年 Ｈ1/3＝3.8ｍ Ｈmax＝7.3ｍ 1982年 Ｈ1/3＝3.63ｍ Ｈmax＝5.95ｍ（途中観測不能） 1997年 Ｈ1/3＝5.01ｍ また、1997年には台風9720号と同程度の波高が台風9707号や9709号の来襲により発生しましたが、このとき真鶴などの西湘海岸には被害がほとんどありませんでした。これらの台風と9720号との違いは、前者が西湘海岸の西方に上陸した台風に対し、後者が房総沖を通過したうねり性の台風であったこと、前者に比べて後者は長周期波が卓越し、しかも強い波群性を有していたことが挙げられます。 討論者 無記名 質疑 ?設計波はどれくらいか？ ?消波ブロックの被害などこれだけ甚大な災害が生じるということは、設計波を越えていなかったのか？ ?生波形をチェックしたか？ ?消波ブロックの移動、大規模突堤の被災を平塚の実測波で説明できるのか？ 回答 当海岸の計画諸元は、沖波波高Ｈo＝6.2ｍ、周期Ｔ＝11.2secとなっています。今回の台風9720号は、平塚の観測波ではＨ1/3＝5.02ｍであり、Ｈmax＝７〜８ｍはあったのではと思われます。生波形についてもチェックをしており、最大1.2ｍに及ぶ長周期の存在や強い波群性を示す波の特性を確認しております。また、県の漁港事務所による検討では、御幸ヶ浜の被災した３０ｔのブロックは今回の高波浪により容易に動くことが推定されています。したがって、今回の波は計画波以上であり、しかも長周期波等が重なり海岸災害を助長したものと判断されます。ただし、平塚の観測波で大規模突堤の被災が説明できるかについては、詳細な検討はしていませんが少し波が小さい気がします。
論文番号 ６７ 著者名 川池健司，井上和也，戸田圭一，林秀樹 論文題目 市街地の高潮氾濫解析法の研究 討論者 今村文彦（東北大学） 質疑 建造物の影響を通過率βを用いて流量を補正することは物理的に正しくないと思われる．建造物による抵抗は運動量の式中に形状抵抗として入れかつ，建造物が占有している影響は，コントロールボリュームの減少として，連続の式に入れるべきである． 回答 本研究においては，建造物の面積が格子面積に対して占有している割合を占有率として定義し，それによるコントロールボリュームの減少を連続式の中で考慮しています．また，建造物による抵抗は，ご指摘のとおり形状抵抗として考慮することも考えられますが，その場合には抵抗係数を同定することが容易ではありません．本研究では，その影響は粗度係数によって評価できると考え，運動量の式中で考慮しています．
論文番号 ７０，７２ 著者名 松本智裕・橋和正・今村文彦・首藤伸夫・小谷美佐・今村文彦・首藤伸夫 論文題目 土石流による津波発生・伝播モデルの開発GISを利用した津波遡上計算と被害推定法 討論者 山下隆男（京大・防災研） 質疑 両論文での遡上計算における粗度や計算法方の相違を示して下さい 回答 両方の論文において、今回改良された波先端条件を用いた遡上計算をおこなっています。一方、粗度に関しては、小谷ら(1998)は、現在の状況での想定津波の数値解析を扱うために、構造物、家屋などを考慮した土地利用に応じた係数を設定していますが、松本ら(1998)は一定係数（小谷らの論文における建物なしの領域に相当）を与えています。なぜなら、松本らの対象は寛永 (1741年)の歴史津波であり、当時、家屋があったとしても木造の構造的に弱いものであり、その地域での密度は低く、考慮しなくともよいと判断しました。一般に、 歴史津波を再現する際には、土地利用などのデータはなくそれを考慮することは大変困難です。ただし、当時は、大きな構造物である防波堤、防潮堤、RC建物、などはなかったので、たとえ土地利用別の粗度を考慮したとしても、高密度市街地を除いてその効果は小さいと判断しています。
論文番号 ７３ 著者名 松冨英夫，飯塚秀則 論文題目 津波の陸上流速とその簡易推定法 討論者 池野正明（電力中央研究所） 質疑 今回提案された流速推定式でパプアニューギニア津波の陸上流速を推定すると，「９ｍ/ｓ」程度になるものなのですか？ 回答 今回提案した流速推定式は平坦地に適用できるもので，平坦地でベルヌーイの定理を用いて推定した流速は今回提案した流速推定式によるものとよく対応しておりました．一方，Sissano Lagoonの砂嘴上やMalolの汀線近くは平坦地の流れでなく，こぶ上の流れであり，適用できないと思われます． ところで，今回の津波はSissano Lagoonの砂嘴上で１０ｍ以上の浸水深に達しました．また，砂嘴上の浸水深や津波高の平面分布から，砂嘴上で流れは常流から射流に遷移したと推定されました．よって，砂嘴上で限界流が生じ，１０ｍ/ｓ以上の流速が生じたと推定されます．
論文番号 ７４ 著者名 池野正明・松山昌史・田中寛好 論文題目 ソリトン分裂津波の大陸棚上での変形とその防波堤設計波圧に関する実験的研究 討論者 鹿島技研 池谷 毅 質疑 Ｑ１；波圧分布（図−１１，１２）は最大波圧なのか，同時波圧なのか． Ｑ２；波圧の提案式によれは，全波圧で考えても静水面付近で波圧分布が折れ曲がると考えてよいか． 回答 Ａ１；図−９に異なる鉛直位置３点での波圧時系列の例を掲載していますが，大陸棚上での浅水変形により段波状となって水面は垂直に切立ち，同時に最大波圧が生じると考えられます． Ａ２；そのように考えています．これは，津波波圧の提案式に限らず，合田式でも言えることだと思います．
論文番号 ７５ 著者名 浅井大輔，今村文彦，首藤伸夫，高橋智幸 論文題目 伊豆半島入間における安政東海地震津波の波高と土砂移動 討論者 柴木秀之 （（株）エコー 環境水理部） 質疑 津波の主周期（沖側周期）と入間の固有周期は？ 回答 津波の主周期は，図-6に載っている図を見て分かるように計算では5分から6分程度である．また，入間の固有周期は，5分程度である． 質疑 第一波とは図-６の時系列のどれを表しているのか？ 回答 図-6における波を１つの波と見なして第一波とする．つまり，図-6に載っている波形全体を第一波とする． 質疑 最大流速が発生する時間は時系列中のいずれの時刻か？ 回答 地震発生から７分後の部分です．
論文番号 ７６ 著者名 藤井直樹・大森政則・高尾誠・金山進・大谷英夫 論文題目 津波による海底地形変化に関する研究 訂正 表−３の実測結果の総堆積量は235,000でなく，725,000が正しい． 討論者 池野正明（電力中央研究所） 質疑 論文中に示された計算式は断面１次元（ｘ座標のみ）モデルですが，気仙沼湾へ適用した際の基礎式（平面２次元）も具体的に追加説明して下さい．（論文中に詳しい記述がないので，討議集に記述して下さい．） 回答 実験は１次元計算ですが，気仙沼ではご指摘のとおり平面２次元で計算していますので関係する式を以下に記述いたします．
論文番号 ８０ 著者名 永澤 豪，田中 仁，松村勝之，山路弘人 論文題目 ADCPを用いた志津川湾内流動の観測 討論者 柴木秀之 （（株）エコー） 質疑 水平方向の流況パターンである湾北流入，湾南流出は回転系の密度流現象として説明できるものなのか．その原因は何か． 回答 このような流況を作る原因として，まずコリオリ力による流れが考えられます．しかし，志津川湾は南北5km，東西10kmの中規模の湾のために，コリオリ力が効くには規模が小さいと思われます．そこで，湾の流動に最も影響を及ぼしている潮流が原因と考えています．湾北部流入・南部流出という傾向は，大潮時，特に水温の成層化の影響が小さい冬期に現れます．逆に，小潮時にはこの流動は弱まるという観測結果が得られています．従って，この流況パターンは潮流と湾の地形的要因が起因すると考えられます． 現在，この湾について数値計算を行っていますが，その結果においても，湾北流入・湾南流出の結果が得られています．この計算においても，コリオリ力よりは潮流と地形的効果が効いているようです．今後，この計算を進めることではっきりと要因を決定したいと考えています．
論文番号 ８３ 著者名 山下隆男 論文題目 ジャワ海における海水流動の３次元シミュレーション 討論者 日野幹雄（中央大学） 質疑（１） この海域の深さはどのくらいですか？bottom stress を計算してからwind stressを入れているが，水深が深いとこの方法の誤差が大きくなるのでは？ 回答 ジャワ海は非常に浅い閉鎖性の高い海域です。東海域はやや深くて６０〜７０m，西海域は２０〜４０m，平均で４０m弱です。 stress の評価法は，まず風によるstressから波浪場をWAM で計算し，波浪場から海面の粗度を与えます。同時に海底のstressの評価にも，波浪の影響を流れとの共存場として繰り返し計算で考慮します。「bottom stress を計算してからwind stressを入れている」のではなく，繰り返し計算で波，流れ共存場のstress を計算しています。ただし，波浪場の計算には流れの影響は考慮していません。 質疑（２） 成層を考慮していますか？ 回答 いません。 討論者 ？ 質疑（１） 海面摩擦の算定に波浪の影響を考慮しているが，従来の摩擦係数にも風速の影響を考慮したものがあります。この方法との相違を示してください。 回答 波浪場を計算しない流れのモデルでは，風速や吹送距離の影響を考慮した海面の摩擦係数を用いることしかできませんが，波浪場の計算を行う場合にはあえて，このような経験的な表示を用いるメリットはありません。波浪場の計算にも海面せん断応力を計算しますので，波浪そのものを粗度として評価することの方が自然です。ただし，この評価方法にも波齢をどのように考慮するかという問題があり，本計算では粗度が波齢の影響を受けないとするCharnock式を使っています。ご承知のように，粗度と波齢の関係については依然として議論のあるところですが，この関係は波浪場の推算結果に影響を与えます。それが流れ場の海面応力に反映されます。波浪場の推算結果は，粗度と波齢の関係によってかなり変わってきますので当然流れ場にも影響するものと思います。風速の大きい場合にはこの差が大きくなります。現在，粗度と波齢の関係による波浪場，平均流場の影響を検討していますが，海面の摩擦係数の経験的な表示との比較は行っていません。 質疑（２） 海底摩擦に波浪の影響を考慮していますが，平均流の計算にradiation stress等の波の力が考慮されていないので，海底摩擦が過大に評価されていませんか？ 回答 風波による鉛直方向に積分したradiation stress勾配による応力場は非常に小さく無視できるオーダーだと思います。ただし，砕波による余剰海面応力を考慮する場合には波浪による余剰応力を考慮する必要があります。しかし，海底におけるせん断応力には波浪は駆動力よりも抵抗力として作用すると考えています。 討論者 余錫平（東京大学） 質疑 波浪場の計算に含まれているnonlinear wave-wave interactionの影響についてどのように理解すればよいですか？ 回答 本モデルではWAMを使用しています。 砕波による余剰海面応力の発生と合わせて波浪場の推算には重要な問題の一つです。 実際にはこの相互作用の評価に波浪場の計算の多くの時間を費やしますので，波浪推算アルゴリズムのスリム化の研究が多くなってきていますので，参考にしてください。
論文番号 ８４ 著者名 八木宏、日向博文、田岡幸司、久木幸二、灘岡和夫 論文題目 短波海洋レーダーに基づく冬季日本海能登半島沖の流況解析 討論者 坂井伸一（電中研 環境科学部） 質疑 ? 吹送流と恒流を分離する際、時間ラグ（位相差）は考慮しているか？ ?恒流計算で対馬暖流を再現しているが、計算の境界条件設定時にＮＯＡＡ／ＡＶＨＲＲなどの広域データを参考にして流量設定を行なっているのか?（対馬第何分岐を想定しているのか?） 回答 ? 現在の方法では、風と流動の位相差は考慮していない。位相差を考慮する方法として応答関数を用いた解析方法が考えられる。今後検討する。 ? 流量は対馬第１分岐流の平均的な流量を設定している。観測期間における実際の流量を与えているわけではない。
論文番号 ８５ 著者名 八木宏、日向博文、緒方健太郎、灘岡和夫 論文題目 長期・広域観測データに基づく鹿島灘沿岸域の大規模流動解析 討論者 小林智尚（岐阜大） 質疑 ? 図―７の温度分布は月平均であるが、実際にはこの領域は黒潮・親潮が混合して動的に大きく変化していると思います。この動的変化が鹿島港近傍の流れに影響をおよぼしているのではないか。 回答 ?確かに、鹿島灘沖の海況は黒潮・親潮の変動に伴いダイナミックに変動している。ただ図―7に描いた温度（密度）分布に基づいて解析した流動は、周期２０日以上のものであるので、数日周期で変動する外洋の海況を考慮しなくても大きな誤りは無いと思われる。
論文番号 ８８ 著者名 田中 仁・長林久夫・山内健二 論文題目 河口感潮域におけるwave set-up高さに関する研究 討論者 上嶋英機（中国工業技術研究所） 質疑 ?p.437 図−２について 小名浜港の潮位との対応について妥当かどうか．測定間の距離が現象を同一化できるのかどうか．例：気圧の変化，風の吹き寄せにの影響 回答 二つの測点距離が１５ｋｍほどあり，確かに気になる点ではあるが，他に使用できるデータが無い．仙台港の場合は距離が近く，その点の問題が少ない． 質疑 ?河口内に滞留した河川水と海水が，波によって河口に閉塞されて河口外（海に）出なくなることがあるのではないか． 回答 実際にそうである．現地の故老の話によると，上陸した台風よりも沖を行く台風の方が氾濫をもたらす危険性が高いとのことである．これは，波による水位上昇の危険性を物語るものである． 質疑 ?約３日間のset-upは長いと考えられる． 回答 図示した結果は特に上昇量が顕著に表れたものを選んでいる．波高が大きい場合にはそれが静穏になるまでの期間も自ずと長くなり，そのために長期間水位上昇が見られる．このように，波の条件によっては長期間続いても不思議はない．
論文番号 ９１ 著者名 山内健二・田中 仁 論文題目 中小河川特有の河口現象を考慮した地形変化予測モデル 討論者 千 受京（東洋建設 鳴尾研究所） 質疑 七北田川河口では年数回の完全閉塞が生じていると報告されているが，この研究における洪水時の地形変化計算の初期値形として開口幅がある程度開いている状態で計算を行っている．もし，完全閉塞した状態での計算をすると，どうなるのか．その予測計算は可能であるかどうか． 回答 基本的には可能と考える．実際，この計算においても砂州のフラッシュは主にoverflowによるものである．今後，計算を行う計画はある． 討論者 高木利光（INA） 質疑 ?通常，砂州フラッシュ直後に河道内の水位が急に低下する現象が見られるが，今回の観測データあるいは計算結果からそのような現象がみられているか． 回答 今回の計算ケースでは，流量が減少する時間帯に満潮となり，またwave set-upも顕著となるために急激な水位低下が見られなかった．潮位変動，set-upのタイミングによっては，ご指摘のような現象が見られる．この点についてはすでに報告を行っている（例えば，水工学論文集，第３５巻，pp.275-280，1991）． 質疑 ?計画洪水規模で水位が３ｍまで上昇したと言うが，この時すでに砂州がフラッシュされてしまっているのか． 回答 その通りである．昨年度の海講では，砂州越流を促進するために砂州の高さを人為的に低減させた計算も行ったが，最大水位に変化は無かった．これは，計画洪水規模では洪水ピーク前に砂州が十分にフラッシュされてしまうことを示している．
論文番号 ９２ 著者名 吉岡 洋，芹沢 重厚，高山 知司，田中 祐志 論文題目 夏季田辺湾における内部急潮による海水交換 討論者 上野成三（大成建設（株）技術研究所） 質疑 湾奥部の海水交換や赤潮の解消にとって，内部急潮による移流と風による混合のどちらが効いているのでしょうか？ 回答 湾口部に内部急潮を引き起こすために，ある程度の湧昇起動風が必要である．それによって湾口部に用意された外洋深層水が湾奥に供給される形態は２種類考えられる．湧昇起動風が強ければ湾内の風成循環+鉛直混合で，弱ければ内部波の形態で，湾奥に外洋深層水を供給して赤潮を解消する． 討論者 田中 昌宏（鹿島建設（株）技術研究所） 質疑 ８／１４前後の風は２〜３ｍ／ｓと弱いですが，沿岸湧昇が起こるのでしょうか？ 回答 観測塔は湾口部にあるので，沖ではもう少し強い風が吹いていたのかもしれない．別の解釈としては，８／１４までは５ｍ／ｓ程度の南風が継続しており，その状態で沖合い底層水が湾口部の海底レベルに達して平衡を保っていた．８／１４前後の風は２〜３ｍ／ｓと弱いがそれ以前の状態から見ると相対的に７〜８ｍ／ｓの逆風といえるので，かろうじて海底レベルで留まっていた沖合い底層水が湾内に進入してきたのではないだろうか．これまで沿岸湧昇といえば，深層水が海面まで達するケースが扱われていたが，本ケースでは躍層が湾口部をクリアするだけの小規模な湧昇である．
論文番号 ９３ 著者名 上野成三，灘岡和夫，高山百合子，勝井秀博（大成建設（株）） 論文題目 湾口シルで砕波する内部潮汐の海水交換能力に関する数値実験 討論者 田中昌宏（鹿島技研） 質疑 （１）塩分の鉛直分布が海水交換量及びパターンに及ぼす影響は？ （２）内部波の砕波の物理的定義は？ 静水圧近似で砕波をどこまで計算できるのか？ （３）現実の対策としてシルの改造を考えているのか？ 回答 （１）塩分分布についてはステップ状の躍層分布と現地に近い成層分布の２通り検討した（本論文では成層分布の結果のみをまとめた）．定性的な海水交換パターンは両者でほぼ等しく，シル高さと海水交換能力の関係も同じ傾向を示した．ただし，定量的には，スッテプ状の塩分分布の方が海水交換能力がやや大きくなった．これは，シルと岸側斜面での砕波によって中間密度の水塊が生成される現象（一種のboundary mixing）が強くなるためと予想される． （２）明確な定義はしていない．計算結果をアニメーションで見て，内部波の波動性が崩れる現象を砕波と呼んでいる．静水圧近似のもとで内部波の砕波がどこまで計算できるかは以下の論文で検討した．上野ら(1998)，斜面上で砕波する内部波の数値計算の検証，土木学会第53回年次学術講演会，p296-297．結論として，内部波の砕波直前の前傾化や伝播速度は計算で良好に再現できるが，砕波後の波形・伝播速度には有意な計算誤差が生じる．ただし，この計算例は非常にきつい密度躍層がついた条件で行った例であるため，数値拡散の影響が大きい．現実的な密度分布での検証が今後の課題である． （３）シルの高さを変えるだけで内部潮汐という自然エネルギーを利用して海水交換を強化できると考えている．本論文は海水交換強化を最適にするシル高さをとりまとめた． 討論者 瀬戸雅文（北海道立中央水産試験場） 質疑 （１）シルと内部砕波・海水交換を考える場合，シルの形状が湧昇と関係して検討要因となるものと考えられるが，形状についてはどのように考えられているのか？ 特に，シルの高さを変化させればシルの湧昇能力も異なってくるものと思われるが？ 回答 （１）シル形状についてはある現地地形を参考にし，高さのみを変化させて海水交換能力を調べた．シルの断面形状については，シルの縦断幅が内部潮汐の１／１０程度で小さいことから，検討パラメータとしなかった．ただし，現地海域の３次元地形効果などを含めたシル形状は海水交換能力に効いてくると予想される．その場合は３次元のフルシミュレーションにより個別に検討するば良いと考えている．
論文番号 ９４ 著者名 宮野 仁 ，柴木秀之 論文題目 湾奥の締切りが湾内の海底地形に及ぼす影響について 討論者 高木利光（株式会社 アイ・エヌ・エー） 質疑 このモデルにより長期的な湾内の定量的な予測は可能なのか．また，このまま浅くなりつづけるのか．どこかで定常的な水深となるのか． 回答 本研究における浮遊泥の移流・拡散モデルでは，河川流及び河川から流出する浮遊泥に関する現地の情報が乏しいことから，モデルの設定条件の妥当性について議論の余地が多々あると考えられる．したがって，出水時の浮遊泥の挙動を定性的に把握することは可能であるが，長期的な，かつ定量的な予測を行うことは，実質的には困難であると思われる． また，論文中の図−５〜７に示すように，現況の底面せん断力は，湾奥の締切り堤建設後に比べて増加傾向にある．これは，締切り堤建設による湾内流速の低下に伴い，湾内における浮遊泥の沈降・堆積量が増加した結果，湾内水深が減少し，締切り堤建設時より湾内流速が多少増加したためであると考えられる．しかしながら，現況においても，巻き上げ限界せん断力0.1N/m２を下回っていることから，河川からの浮遊泥が湾内に沈降・堆積しやすい環境にあると考えられる．将来的にも，潮流，波浪，河川流などの外力と底質及び浮遊泥の流出量のバランスが保たれるまで，湾内水深の減少は進行すると思われる．
論文番号 ９５ 著者名 Mohammad Dibajnia, 樋川 直樹, 渡辺 晃 論文題目 長周期波を含む非対称不規則波浪下でのシートフロー漂砂 討論者 岡安章夫（横浜国立大学大学院工学研究科） 質疑 砕波帯内等で拘束長周期波の波群に対する位相が変化した場合（厳密には「拘束」ではないが、波群に依存するという意味）に、漂砂量はどのように変化するのか？ 回答 長周期波の拘束が解かれた場合，その波群に対する位相によって漂砂量は大きく変わる可能性がありますが，砕波帯内では戻り流れが支配的なので沖向き漂砂が岸向きになるまでには至らないと考えられます． 討論者 佐藤慎司（建設省 土木研究所） 質疑 短周期波成分の波形の非対称性はどのようにしてモデル化したのか。 回答 短周期波成分の波形データは，不規則波の浅水変形の実験において波が砕波する直前の場所で計測されたものを直接用いました．ただし，波形データからは定常及び長周期成分を取り除いてあります．
論文番号 ９６ 著者名 灘岡和夫、二瓶泰雄、中村則保 論文題目 非対称振動流場におけるシートフロー状流動層の乱流構造に関する研究 討論者 浅野敏之（鹿児島大） 質疑 対称波と非対称波の移動状況を見ると、移動開始時においても対称波では粒子群が浮遊状態にあるのに対して、非対称波では底面粒子群にパックされた状態にある。著者らは両者の差を形成される渦サイズで説明しようとしているが、底面付近の粒子かみ合わせなどの状況がかなり違うのでこれらの結果に出ているのではないか？ 回答 ゼロアップクロス位相では、対称波では、前の半周期で巻き上がった粒子が浮遊状態にあるのに対して、非対称波では、浮遊粒子はほとんど見られない（図２、３）。これは、主として前の半周期間における粒子移動特性の違いが顕著に現れているものと考えている。すなわち、対称波では、減速域において発達した大規模渦構造により大量の粒子が鉛直上方へ巻き上げられるのに対して、非対称波では、負流速位相においては、粒子沈降が支配的であることから（図７）、ゼロアップクロス位相において浮遊粒子が存在しないものと考えられる。このような結果は履歴効果の一つであり、非対称振動流場の特性が顕著に現れているものと考えられる。なお、このようなゼロアップクロス位相における現象に関しては、討論者が指摘しているような渦構造と関連づけた説明は行っていない。
論文番号 ９７ 著者名 Mohammad Dibajnia, 高沢 大志, 渡辺 晃 論文題目 混合粒径における移動層厚と漂砂量に関する研究 討論者 柴山智也（横浜国立大学大学院工学研究科） 質疑 実験結果では粗砂と細砂で移動方向が異なる場合が見られるが，このような場合についても無次元漂砂量(正負の符号を含む)は例えば式(6)のような形式で説明可能なのですか？ 回答 論文中の式(6)または式(7)は混合砂の中の粗砂だけを対象した漂砂量式で細砂分は含まれていません．混合砂の移動には本論文で対象としたものとは異なった機構もあるので，より広範囲条件に適用できる漂砂量式の開発にはさらに研究を続ける必要があります． 討論者 辻本剛三（神戸市立工業高等専門学校都市工学科） 質疑 混合率で底質の特性を扱う時に通常の偏わい度や淘汰係数との関連をどのように考えていくのでしょうか？ 回答 今回の実験に用いた混合砂は基本的な移動機構をつかむために2種類だけの均一砂を混ぜて作成した bi-modal のもので，ひろがりがあるような分布をしていない．より一般的な混合砂を扱う場合には，混合率の他に偏わい度や淘汰係数等も考慮する必要があると考えられる．
論文番号 ９８ 著者名 李 在炯，入江 功，村上啓介，佐藤愼司 論文題目 大水深域を含めた広域の漂砂特性?底質特性情報の分析に注目して? 討論者 柴山知也（横浜国立大学） 質疑 底質分析から明らかになったのは，漂砂の供給源が共通であるということで，大水深で互いに連結していることを示すには，波による移動限界・流れなどを検討する必要があるのではないか？ 討論者 佐藤（土木研究所） 質疑 漂砂源の推定，漂砂の卓越方向が検討できるように，河川や崖の鉱物組成の情報も含めて議論して欲しい．
論文番号 ９９ 著者名 酒井哲郎・後藤仁志・松原隆之・高橋智洋 論文題目 非対称砂漣上の浮遊過程における一方向流と水圧変動の役割 討論者 辻本剛三 質疑 水圧変動から得られる移動機構の情報は，底面掃流砂量の算定の時の限界シールズ数などに適用されるものなのでしょうか． 回答 適用すべきではないかというのが，この研究の意図するところです．しかし，水圧変動効果が効く条件にはある程度制限がありますし，効果の大小は同一粒径の砂を対象に考えても砂の飽和度によっても影響を受けます．従って，本研究の結果は，従来の底面せん断力を基準とした海底床形態の分類を全面的に否定するものではありません．ある種の底質条件では，底面せん断の力に加えて水圧変動効果の影響が考慮されるべきではとの問題提起と受け止めていただければと思います．
論文番号 １００ 著者名 辻本剛三 論文題目 浮遊砂濃度フラックによる２次元海浜地形変化に関する研究 討論者 栗山善昭（運輸省港湾技術研究所） 質疑 本モデルにおいて砕波点近傍で何故乱れが大きくなるのか お教えいただきたい 回答 本研究では標準なｋーε乱流モデルを用いて乱流諸量の算定を行っています。 乱流モデルの乱れの生成項は、速度の勾配や歪みによって評価されるため、砕波点近傍ではこれらがきわめて大きな値を有するためです。ただ、計算上は自然発生的に乱れが砕波点近傍で生じていますが、初期値として乱れには微小な値を与えております。今後は、人為的な初期値を与えることなく乱れの発生の検討を加えたいと思います。