最終更新時:
論文番号 1
著者名 梅山元彦
論文題目 変調性進行波列の過渡状況有限振幅波理論
訂正
文中の定住波を定在波にする。
討論者 浜中健一郎(北海道東海大学)
質疑
周波数に関する高次項は、無限時間ではどの様な振る舞いをするのか。時間的に振
動するのか。上と同様に高次解は造波板の近傍ではゼロになるのか。ならなければ造
波板の動きと流体の動きに矛盾が生じないか。
回答
干渉波の高次項である三次オーダーの水面変動量は式(34)に示してあり、項数
が多いために一見煩雑ですが、大きく分類すると三つのタイプがあることがわかりま
す。一つ目はうなり現象を表す定在波であり、二つ目は進行性の干渉波であり、三つ
目は進行性干渉波と周波数および波数が等しく反対方向に伝搬する後退性の干渉波で
あります。質問者はこのうちの定在波が時間の経過に伴ってどのように振動するかを
質問していますが、図ー1〜4の実験結果から判断してこの項が時間経過に伴って水
面の鉛直変動に影響を与えているようには見えません。従って、この成分は初期段階
でその役割を終えたものとして扱うことが適切であろうと考えて、今回の理論計算に
おいてはある時間より後はこの項は計算から除外しています。運動が安定した後は、
三次オーダーの進行性干渉波と後退性干渉波だけが波群の構成に関与するものとして
計算を行います。今回の実験条件では、いわゆる数学的な定常が達成される前に運動
が安定する傾向にあります。その安定が定常になる前に起こるという理由から過渡状
況という仮定で理論展開を行っており、完全な初期値問題とは異なっています。
討論者 富田孝史(運輸省港湾技術研究所)
質疑
実験結果を用いて理論を検証する際、どの様に摂動パラメーターや一次の振幅を決
めるのですか。もくろんだ波高や周期をもった波を理論的に検証するときに摂動パラ
メーターなどのインプット条件をシステマティックに決める方法についてご検討され
ていれば教えていただきたい。
回答
実験では任意波形発生装置で電気的に合成した cos 信号を重ね合わせることによ
って造波板を動かしており、その結果発生した波を進行波 I と進行波 II が伝播過
程で重ね合わさって波列ができたものと仮定しています。実験結果の時間波形をフー
リエ解析することによって進行波 I と進行波 II の主周波数および三次オーダー周
波数の位置において卓越するスペクトル成分が現れます。理論計算では主周波数の位
置に現れたスペクトル成分から二つの進行波の振幅 aI、aII を想定します。次に、
進行波 I と進行波 II の波長 LI、LII は水深がわかっていますから計算できます。
式(19)と(20)に示されているように、摂動パラメーターは二成分波問題であ
ることを考慮すれば、eI = 2paI/LIとeII = 2paII/LII が混在することがわかります
。理論計算の入力条件については今のところスペクトル解析結果を第一次近似として
、最終的には実験結果を適正に表すまで入力条件を変えて計算を続けます。理想的に
は進行波 I と進行波 II を別々の水路で造波させて途中から同じ水路内を伝播させ
るような実験ができれば入力については何ら問題は生じないのでしょうが、そのよう
な実験施設は持ち合わせませんので、試行錯誤して入力条件を決定しています。
討論者 大山巧(清水建設株式会社)
質疑
理論を検証するための実験を行っていますが、理論仮定と実験条件の整合性に問題
があると思います。理論ではあくまでも非線形干渉の結果として得られる波動場を対
象としているため、基本成分(一次オーダー成分)自体の性質が実験で造波している
ものとは異なっています。さらには、実験において線形波動理論に基づく造波を行っ
ているとすれば、造波時の寄生自由波の影響も現れるはずです。実験で理論検証をす
るためには、干渉後に得られた波動場から自由波部分を抽出し、それを一次オーダー
成分として、二次、三次の拘束波を理論より求めた後、それらを実験結果と比較する
必要があるでしょう。検証の方法としては、他の理論解(多成分の非線形干渉につい
ては四次オーダーまで求められています)との比較でも良いかと思います。
回答
この研究は、水槽内で造波された波が三次オーダー非線形進行波 I と三次オーダ
ーの非線形進行波 II が合成された結果生じたものであるという仮定がなされていま
す。実際に理論の整合性を確かめるためには、前の
回答のところ述べたような実験が
行われなければなりません。しかしながら、電気的に合成された二波の合成信号で造
波板を動かしても、ダブルフラップを用いて行った二成分波の実験で見られるのと同
様な変調現象が現れています。今回の論文では主に波列が水路上でどのように変調し
てゆくかを理論的に解明しようという目的ではじめましたが、今まで摂動理論では得
られなかった変調現象を理論的に説明することには成功しています。基本成分の性質
が非線形干渉の結果変わることは、式(21)と(22)で考慮しています。この結
果、非線形進行波 I と II の波数も変化します。このことはページ数の制約から本
論文では省いてしまいましたが、計算上はそのような処理を行っています。次に、多
成分波の四次オーダー非線形理論で今回の実験結果を議論することはできないと思わ
れます。ご指摘の解においては波と波の間のエネルギー輸送が考慮されていますが、
今回の実験はエネルギーの輸送が起こらない範囲で変調を議論しています。
討論者 間瀬肇(京都大学防災研究所)
質疑
導いた理論解で、波群の再帰現象や包絡ソリトンへの移行が説明できるか。
回答
運動が安定した後、干渉波の三次オーダーの波として進行波(拘束波)と後退波(
自由波)が残ります。後者は進行方向こそ前者とは逆ですが、周波数と波数は同じな
ので、お互いが重なり合って重複波のような振る舞いをします。その結果、理論解は
必ず再帰性を示すことになります。今回の実験条件の範囲では包絡ソリトは空間にお
いても再帰性があり、ある一定距離離れると同一の時間波形になることは理論から容
易に証明できます。
論文番号 2
著者名 合田良実、賀川真有
論文題目 造波水路内の波峯分裂のメカニズムについて
訂正
発表論文で造波境界条件をx = 0で与えたのは不適切であり、造波板の各瞬時の位
置で与えるよう修正した結果、式(12)に新規項が追加され、図−1〜3を差し替え
る必要が生じた。また、式(23)にも誤りがある。アメリカ土木学会主催のWAVES '9
7で発表した“Recurring Evolution of Water Waves through Nonresonant Interact
ions”を参照していただければ誠に幸いである(合田宛に論文コピーを請求されたい)。
討論者 浜中建一郎(北海道東海大学)
質疑
高次・低次の成分波間にエネルギーのやりとりがないと結論づけているが、どのよ
うなときにエネルギーの授受があると考えているのか。
回答
Madsen・Sorensen(1993)は、風波の発達時に見られるようなtriad interactionを
想定しているので、そのような現象ではないことを検証したものである。
討論者 後野正雄(大阪工業大学)
質疑
造波型式がフラップ型とピストン型で2次波峯あるいは自由波の振幅はどのように
変化するのか。
回答
今回はピストン型造波型式についてのみの解析である。しかし、既往の研究によれ
ばh/Lが小さいところでは両型式の間にはほとんど差異がないけれども、h/Lが0.2〜0
.3の領域ではフラップ型による自由波振幅がやや小さいようである。
討論者 森信人((財)電力中央研究所)
質疑
1)深海域へ漸近したとき(kh→∞)の解のふるまいはどのようなものか。
2)NLSの不定性の限界との関係は?
回答
1)今回の理論展開では深海域へ漸近するにつれて2倍、3倍周波数成分が増大す
る傾向をみせているが、既存の研究と比べてやや異なるところがあり、さらに吟味す
る必要があるかと思われる。
2)NLSについては特に検討していないので、的確なお答えができない。
論文番号 3
著者名 大山 巧・土田 充・川口 隆・鈴木志人
論文題目 非線形波動場を対象とした自由波制御型無反射造波法
討論者 青木伸一(豊橋技術科学大学)
質疑
不規則波を用いて構造物の実験を行う場合、構造物との干渉により生じた長周期自
由波の造波側ビーチでの再反射を防ぐことは難しいと思われる。これに対処するため
には、ピストンやフラップ型の方が制御が優れていると思われるが?
回答
問題を造波装置と消波装置に分けてお答えします。
まず、造波装置に関しては、本研究で対象とする波動場が非線形不規則波であるこ
とから、ピストンやフラップ型による反射波制御は現時点では困難であると考えます
。これを克服するには、1) 非線形干渉を考慮した不規則波の反射波制御理論を構築
すること、2) その理論に基づくリアルタイム制御を可能にすること、が必要になり
ます。これに対して、本研究で用いた鉛直振動流方式の造波法は、何等の制御を行う
ことなく非線形不規則波をほとんど再反射させない点に利点があると考えています。
水路両側の消波装置については、ここでは砕石を緩傾斜で配置した通常の消波装置
を用いています。論文中で紹介した2成分波では、拘束長周期波の周波数が個々波の
平均周波数の1/4と比較的大きいので、砕石による消波装置でも十分な消波性能が得
られることを確認しています。しかし、対象とする長周期波がさらに低周波数になり
波長が長くなると、砕石などによる乱れ・砕波による消波では十分な性能が得られな
くなります。この点については、現在の消波装置の背後に長周期成分を反射させない
何らかの工夫をすることにより、改良していく予定です。
論文番号 5
著者名 和田 清・Harry Yeh
論文題目 斜め入射する孤立波の変形とrunupに関する実験的研究
討論者 都司 嘉宣(東大地震研究所)
質疑
1)この実験のMach stem は,反射面に対して入射波,反射波が対称であったか,
非対称であったか.
回答
孤立波の入射角に応じて,反射面に対する対称性は異なってくる.本実験では,入
射角30度に固定しており,入射波と反射波は非対称である.Mach stemの波峰線を連
ねた軸に対して,入射波の波峰線の角度が反射波のそれよりも大きい状態であった.
質疑
2)Mach stem の部分はローカルには soliton の安定解とはなっていないはずであ
る.すると soliton 分裂が起きるはずであるが,それは観察できたか.
回答
図-3に示したように,鉛直壁付近には顕著なMach stem が形成されたが,水深波高
比(H/h)が0.05-0.22の範囲ではsoliton 分裂のような現象は観察されていない.波
高計の測定範囲の関係で,Mach stem についてはH/h>0.22のケースについては実験を
行っていない.非線形性が増加すればsoliton 分裂が顕在化する可能性はあるものと
思われる.
討論者 森屋陽一(五洋建設(株)技術研究所)
質疑
1)Mach stem は十分発達するまでにかなり長い伝播距離が必要ですが,計測地点
でのMach stemは十分発達した状態なのか.
回答
論文中に明記しているように,波高計の計測範囲はガラス面から汀線方向x=124c
mの距離まで行った.論文や発表中に用いたデータは,ガラス面から24cm離れた位置
における結果である.それ以外の測定範囲でも,レーザー光を用いた画像計測手法(
Laser-Induced -Image Water Surface Profiler System)を同時に行っており,現在
,波高計のデータと併せてのMach stem などの発達過程を解析を行っている.今の所
,x=24cmと124cmにおける岸沖方向の時間波形はほぼ類似していることが確認され
ている.
質疑
2)Mach stem の伝播による発達の様子は実験において観察しているか.
回答
写真,ビデオ画像からMach stem の伝播による発達の様子は観察されている.また
,上述したように,波高計による点計測だけではなくスリット状のレーザ光を用いた
水面変動の線計測を,汀線に平行および垂直な方向に十数測線設定して,画像解析に
よる定量化を行っている最中である.
論文番号 6
著者名 郭文秀, 西村仁嗣
論文題目 Green関数法による任意水深水域の波浪場解析
討論者 浜中健一郎 (北海道東海大学)
質疑
素解を数値的に求め、境界要素法を適用するという2段階構成となっているが、そ
れでも他の解析法に比して利点があるか。
任意の地形に対し、必ず素解が得られるのか。
回答
利点の第一は、回折の効果が極めて正確に把握される点である。他の手法ではとも
すればこれが過小評価され、危険側の結果を得ることに留意されたい。第二は、計算
方法が簡明であり、誰が計算しても同じ結果が得られることである。境界条件の取り
扱いなどに恣意性が割り込む余地が殆どないからである。第三に、緩勾配方程式を差
分化して解くのに比べると、計算労力が小さくて済むことが挙げられる。素解や境界
接続の計算は、反復計算の初期に一度だけ行なえばよい。
極端に複雑な地形が与えられた場合、計算精度に問題を生じることは当然あり得る
。いずれにしても、点源から半無限領域に広がる進行性の円環波を求めるだけなので
、この解が得られないようではいかなる解析法も適用できないであろう。
討論者 岩崎敏夫 (東京久栄)
質疑
点波源の配置の仕方はどうなっているか
波源強度の分布はどうしたのか
回答
点波源は一波長当り10数個、等間隔に配置すれば十分である。ただし、狭い開口部
等では、地形的な要因も考慮する必要があろう。それ以上の波源を配置しても、計算
結果に有意な差は生じない。
波源の強度と位相の分布は、すべての境界条件を満たすよう繰り返し計算によって
決定する。これが本計算の主要部分である。開境界に関しては、一度だけ簡単な積分
方程式を解いて(数値的にはマトリックス演算により連立1次方程式を解く)決定する
必要がある。その具体的な定式化については、参考文献に掲げた海岸工学論文集第40
巻の西村らの論文に述べられている。
これらの基本的な問題については、「ながれ」次号に掲載予定の同著者の論文に、
さらに詳細に記述されている。
論文番号 7
著者名 林 雄一郎,田中 仁
論文題目 急拡を伴う平面波動場の数値解析〜ブシネスク方程式と乱流モデルに基づ
いて〜
討論者 佐藤 愼司(建設省土木研究所)
質疑
(1)拡散項を考慮しない計算結果との比較は検討されているか.
(2)図−11で,急拡の前にも乱れエネルギーが生成されているのは何故か.
回答
(1)Boussinesq方程式は,その適用範囲として波動場のスペクトル帯域が狭い場合に
限定される.一方,本研究で用いた実験水槽では壁面近傍に吸収体を設けていないた
め,急拡を波峰が通過した後,十分時間が経過した場合には,反射波により非常に複
雑な波況になる.したがって従来のBoussinesq方程式では任意のスペクトルを有する
不規則波動に対応できないのか,計算上不安定になりやすく,有意な比較・検討をで
きなかった.
(2)乱流エネルギーkの輸送方程式(8)中,鉛直成分フ生成項Pkvは,次式で表される.
Pkv=Ck・U*3/D
ここでCk=1/√Cf,Cf=gn2/D1/3,g:重力加速度,n:マニングの粗度係数,D:全水
深,U*:摩擦速度である.これより分かるように自由せん断流が形成されていなくて
も,底面摩擦によりkは生成される.
討論者 灘岡 和夫(東京工業大学大学院情報環境学専攻)
質疑
(1)図−10の流速ベクトル図を見ると,急拡部での流れの剥離,渦の生成が十分に表
現できていないように見えるが,その点についての実現象との比較についてコメント
をお願いします.
(2)乱流量の側壁での境界条件についての取り扱いが重要になると思いますが,その
点についてコメントをお願いします.
回答
(1)実験では急拡を過ぎる流れによる剥離渦や戻り流れによる渦の移動等が観測され
ている.定性的な考察は参考文献中で成されているが,ご指摘のあったとおり今後計
算結果を踏まえた定量的な比較が必要であると考えている.
(2)実験水槽の初期状態は静水であるからkとεは0と考えるが,計算の初期条件とし
ては不適当なため,0でない値を設定している.すなわち計算上流体が動いていない
ときもある値を持つことから,壁面でnon-slip条件を与える際にもこの値を用いている.
討論者 浅野 敏之(鹿児島大学工学部)
質疑
急拡地形の波峰方向の変動はBoussinesq方程式で記述できるか,散乱波成分が現れ
ないか.
回答
方程式系は2次元の正対称の形をしているので波の進行方向に支配される因子は少
ないと予想される.ご指摘の散乱波成分が発生しているか確認はしていないが,流速
の局所的な分布に大きな速度勾配が生まれる箇所があれば運動量は2階微分の項によ
り拡散されるので,波高もそれに従うと考えている.
論文番号 8
著者名 間瀬 肇,北野利一,吉岡 洋
論文題目 不規則波のハイブリッド非線形平面変形モデル
討論者 森 信人(電力中央研究所)
質疑
KP方程式は波の交差角が小さくないと使えないが,円錐浅瀬の背後で波が屈折して
交差角が大きくなる場合の妥当性は? また適用性は?
回答
使えないということに関しては,1)解が発散して使えない(答えが出ない),2
)適用範囲外,の意味があるが,質問は 2)と思われる.円錐背後の波向きについ
ては計算してないので,角度の大小に関する適用性については検討していない.理論
の適用範囲は,通常の放物型近似方程式のように,主波向きからプラス,マイナス3
0度以内と考えられる.もちろんそれより大きな角度になっても計算結果は得られる
.また,規則波の場合とは異なって,不規則波の場合には計算結果はなまって(平均
化されて)出るので,適用範囲外の計算を行っても実験結果との対応はそれほど異な
ったものにはならないと思われる.
討論者 佐藤慎司(土木研究所)
質疑
本計算モデルで長周期波成分の発達は計算できるか? できるとすれば,図9に示
されている平均水位の変化も計算できるのではないか?
回答
長周期波の成分の発達,および高周波成分の変化の計算はできる.しかし,平均水
位の変化は計算できない.それは,水位変動をフーリエ級数表示する際,振動成分の
みで表しており,これらを時間平均すれば0になるからである.平均水位の変化を含
めるためには,時間に依存しない項を入れなければならない.以前その項をいれて式
の誘導を行ったが,高次の項として無視されたという結果を得た.これについては,
今一度検討してみたい.
討論者 喜岡 渉(名古屋工業大学)
質疑
複素振幅の計算から,時間波形を求めるためにはどのようにすればいいか? あく
まで関係式(11) を使うのか,微小振幅波の式(20) を用いるのか?
回答
複素振幅 An は式(19) で計算されるが,ここでは分散項の修正の効果が入ってい
る.時間波形を求めるためには,式(16) に戻ってみると,計算された An に場所に
よる位相の変化を考慮しなければならないので,式(17) の 波数に関する積分を引数
とする指数関数を乗じなければならない.その波数の計算には式(11) を用いる.こ
うして場所の補正をした An を逆フーリエ変換することによって時間波形を求める.
論文番号 9
著者名 金山 進
論文題目 強分散性非線形平面波浪場に対する多層モデルの提案
訂正
式(6),式(12),式(24)にミスがあり,正しくは以下の通り.
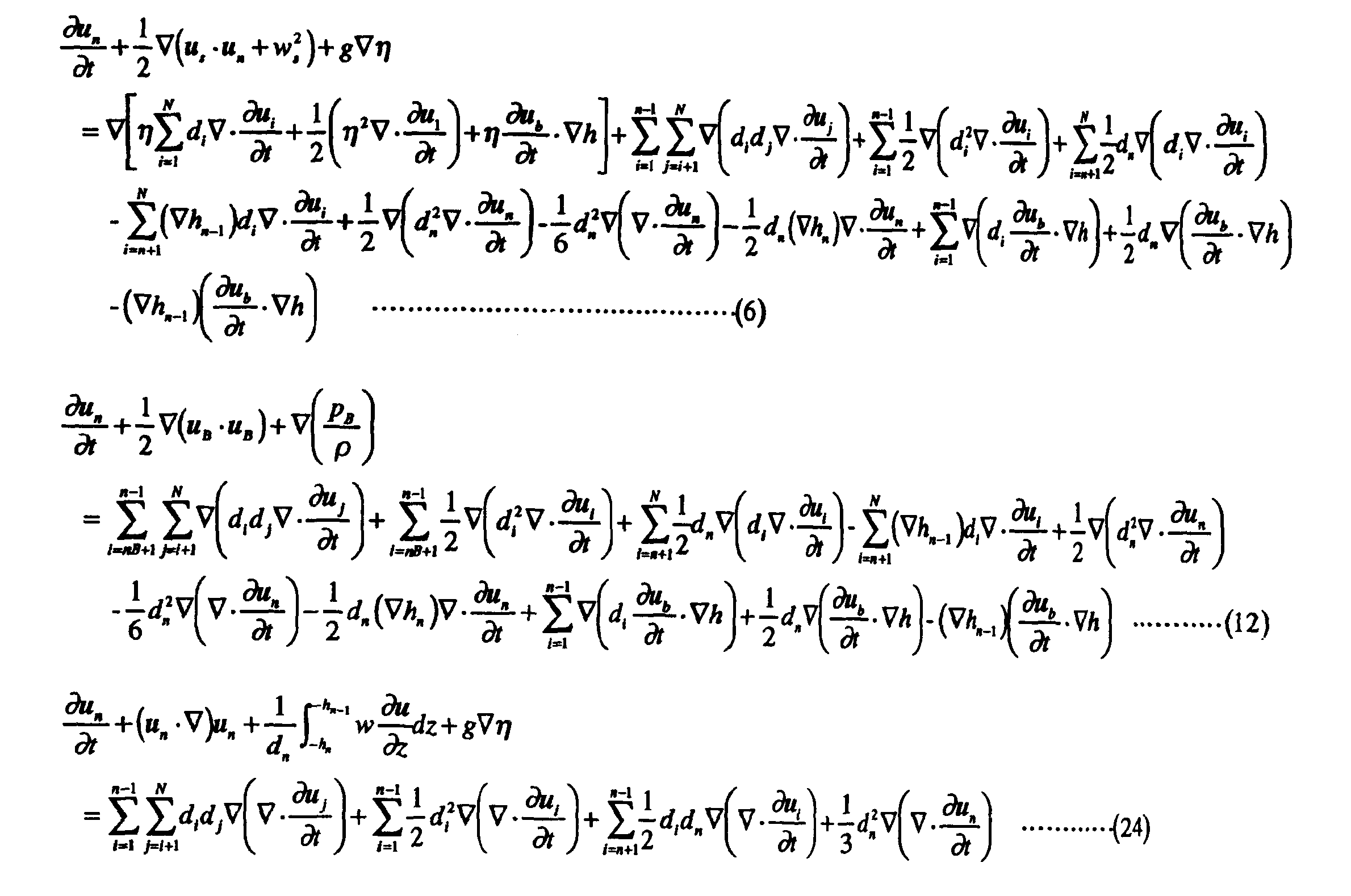
討論者 大山 巧(清水建設 技術研究所)
質疑
図−3,測点P5における不一致は修正Boussinesq方程式であるNwoguのモデルに
も同様に認められた(Ohyama et.al.:1995).本モデルの場合もそうだが,長波近
似方程式の分散関係を修正できたとしても,基本的仮定は長波であるため,自由波と
拘束波間のエネルギーの移行が高周波数領域でうまく表現されるかについては未だ議
論の余地があると思う.
回答
本モデルに限らず,最近の高次近似長波モデル(Kirby・Wei:1994,Gobbi・Kirby:
1996 等)は分散性については近似を行うものの,非線形性についてはその分散性
の精度の範囲内ではフルに評価しており,分散性の精度とともに2次の非線形干渉の
精度も向上していることが示されています.本モデルの場合は図−2がこれにあたり
ます.分散関係のみを単独に改善しているのではないことを一応強調させて頂きます.
測点P5での不整合が2次の非線形の産物である拘束波とこれが解放された自由波
が再び搬送波と干渉するといったいわば3次の現象に対する精度の不足に因るもので
はないかという点は,全く御指摘の通りで,3次の非線形性に対する本モデルの精度
については検討の必要があると思います.
論文番号 10
著者名 E.C.Cruz、石倉正英 、青野利夫
論文題目 非線形分散波モデルを用いた開境界処理に関する研究
討論者 東北大学 真野明
質疑
図7(a)の計算において、エネルギー吸収帯を外周部全域に設置したと書かれてあり
ますが、この図の上側の境界で、波が境界に沿って伝播するような場所にエネルギー
吸収帯をおくと、波の場が非一様になって、吸収帯の方へ回折するような結果になり
ませんか?入射角が境界に立ってた法線から測って90°の場合の、エネルギー吸収
帯の計算の方法を教えて下さい。
DISCUSSION
The apparent existence of diffraction effects at the offshore absorption r
egion (upper boundary) is attributed to the damping term (u in Eq.(2). This
is an unavoidable consequence of the use of the sponge layer in horizontally
2D computations. However, the interior of the calculation region is generall
y only minimally affected by the wave field in the peripheral region because
the following steps have been taken in the numerical implementation of the m
odel equations:
(1) The damping term acts only on the outgoing wave fields in order to sati
sfy the radiation condition at the open boundaries at all sides of the domai
n. In the interior of the computation, (=0 so that any processes there are p
hysically caused by the interior. This entails a careful discretization of t
he model equations at the boundary of the interior and the damping regions,
especially of the nonlinear terms.
(2) The wave field in the damping region, which is transformed artificially
by numerical damping, is still forced at the outer edges of the damping regi
ons to satisfy the necessary absorbing boundary conditions for multidirectio
nal waves, as a result of the directional dispersion in the damping regions.
These conditions are obtained using the linearized forms of the model equati
ons together with a first-order expansion of the frequency-related and direc
tion-related wave parameters. For the multidirectional but monochromatic wav
e fields shown in Figs.7 and 8, the required conditions are as follows:
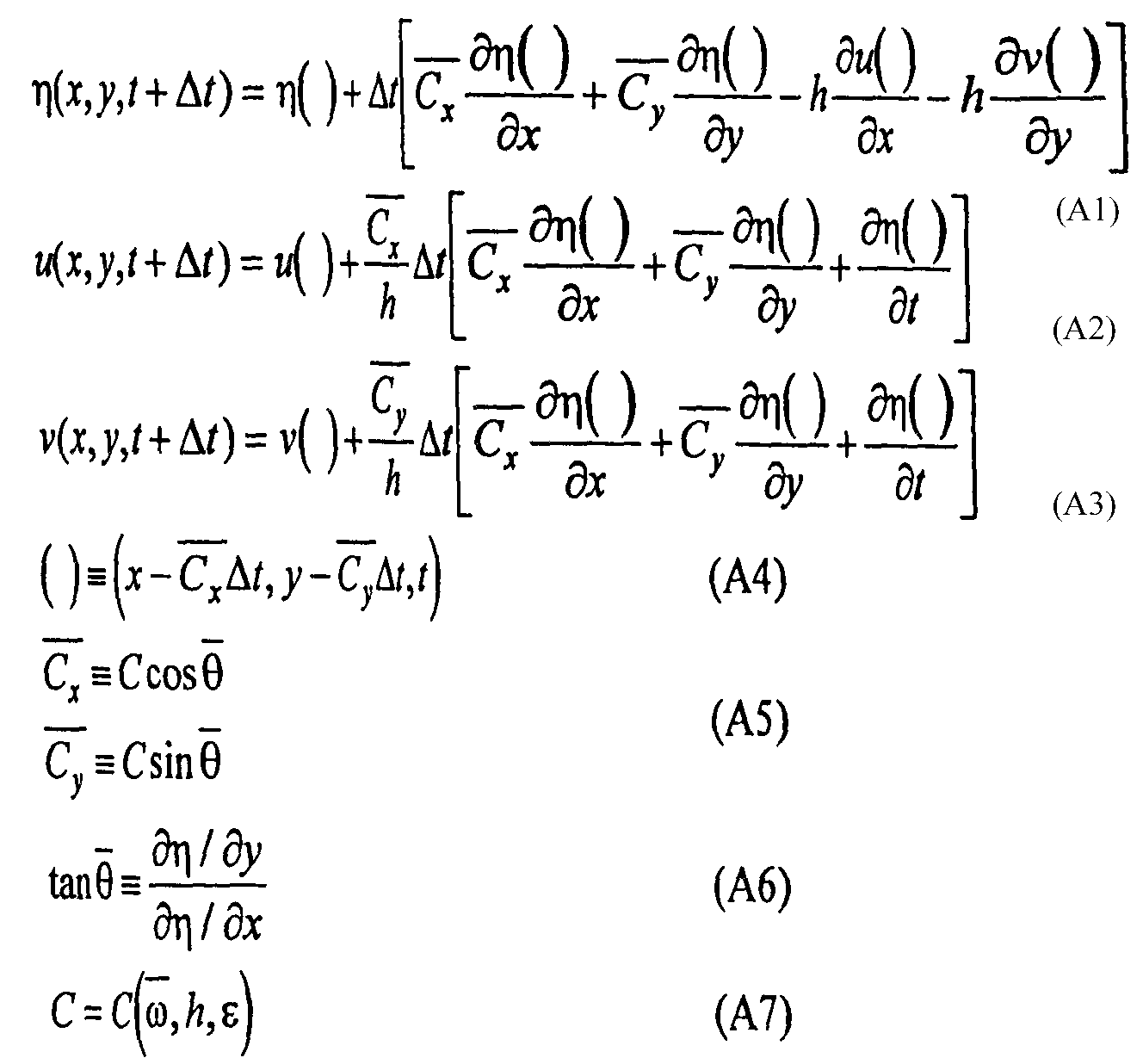
Eqs.(A1)-(A3) express the condition that the value of ( or velocity at the e
dge (open boundary) at the current time step is dependent on the variables a
t a certain tributary point at an earlier time. This point is spatially loca
ted according to Eq.(A4). C is the wave celerity and is the wave direction
as computed from Eq.(A6). The celerity is a function of the representative f
requency , local depth h and the damping coefficient ( at the edge. In deriv
ing these conditions, the following assumptions were made:
(1) sinusoidal wave
(2) uniform depth
(3) all deviations of the frequency- and direction-dependent wave component
s of second-order and higher were neglected.
The development of absorbing boundary conditions for the more general multi
directional random wavesto be used in conjunction with Boussinesq models, to
gether with detailed discussion of the numerical model, will be the sole sub
ject of a paper being prepared for an English journal, hopefully to appear t
his year.
論文番号 11
著者名 平山克也,平石哲也,灘岡和夫,清川哲志
論文題目 新しい非線型波浪モデルに対するエネルギー減衰評価方法の検討
訂正
(12)式にミスがあり、左辺第2項に Cp2 を乗じ、右辺第1項の{ }の前のq0を
削除する のが正しい.
(16)式にミスがあり、左辺第6項はβu0xではなく、βu0xtが正しい.
(22)式にミスがあり、左辺第1項の( )の後ろに添え字xを付加するのが正しい.
P52左段1行目のエネルギー減衰項の表現にミスがあり、εqではなくεqsが正しい.
P52左段2行目の底面摩擦項の表現にミスがあり、f|q|qではなくf|qs|qsが正しい.
討論者 真野明(東北大学)
質疑
(1)(9)式の底面摩擦項が、表面流速q0を使って表現されています.この波浪モデル
は浅水から深水までの広い領域をカバーすることを目指しているようなので、このよ
うな表現では、摩擦係数の中に表面流速と底面流速の変換係数が入り込み厄介になり
ませんか?
(2)図−9等において、非線型緩勾配波動方程式と非線形狭帯域波動方程式では有意
な差があるようですが、理由を教えてください.
回答
(1)本研究で用いた波浪モデルは、波の弱非線形性および弱分散性を仮定して導かれ
たものです.そのため本モデルの基礎式は、Boussinesq方程式と同様に単一の流速成
分(本モデルでは表面流速q0)のみで表現されており、大まかには流速の鉛直依存
関数と対象波の設定波数が異なるのみとなっております.したがって本モデルにおい
て底面摩擦項を表現する際には、Boussinesq系のモデルで頻繁に行われているように
、単一の流速成分を用いて表現する方法が適用できるものと考えられますので、ご指
摘のような問題は回避できるものと考えます.
(2)ご指摘のように、図−9および図−10をみると、とくに球面浅瀬上において両
者の波高分布に有意な差が見受けられます.これは、非線形緩勾配波動方程式の誘導
過程において、緩勾配近似などいくつかの仮定を用いたことと関係しているのではな
いかと推測されます.なお本研究で用いた非線形緩勾配波動方程式は、連続式と運動
方程式で表される非線形狭帯域波動方程式を、いくつかの仮定のもとに摂動法と緩勾
配近似を用いて1つの式にまとめたものです.
論文番号 12
著者名 安田孝志・陸田秀実・小笠原敏記・多田彰秀
論文題目 リーフ上のクノイド波の砕波特性
討論者 信岡尚道(茨城大学)
質疑
ジェットサイズを波速,波形,水面の水粒子速度などのパラメータから評価できる
のでしょうか?
回答
孤立波の場合であれば,ジェットサイズを入射波およびリーフ条件より一義的に決
定できますので,砕波限界時の波速などと関係付けることは可能です.これを理論的
に行うにはジェット生成の動力学理論が必要ですが,今後の課題です.
討論者 浜中建一郎(北海道東海大学)
質疑
強い干渉が存在すると主張しているケースでは,単に2次波峯と主波峯が同一地点
に達したときに砕波する様に海底地形が作られているだけではないのか?
干渉が存在すると主張するには,どのような干渉なのかを説明する必要があるので
はないか?
回答
指摘のように,海底地形をダブルリーフとすることで2次波峯を発生させ,主波峯
と2次波峯との一体化によって複合型砕波を生成させている.
これは,強大なジェットを伴う大規模な砕波を発生させれば波高減衰が著しく低下す
るという考えに基づいており,リーフによる波浪制御を行う場合,このような考え方
が重要であることを意味している.
また,複合型砕波のジェットサイズは従来型砕波の3倍以上にも及び,一般的なシ
ングルリーフでは複合型砕波ほどの大規模な砕波を発生させることは不可能であるこ
とが著者らの研究で既に明らかにされている.
このような大規模なジェットの生成には主波峯と2次波峯の一体化が不可欠であり,
通常のシングルリーフによるジェットサイズを単純に加え併せた以上のジェットサイ
ズにまで達するため,これら両波峯間において砕波限界時に何らかの相互干渉が起き
ていると著者らは考える.
詳細については,既に論文で発表済みである.
質疑
強い干渉が存在すると主張している場合,2次波峯の砕波と主波峯の砕波を合わせ
たより大きな砕波が起こると言うが,この場合,同一条件で2次波峯だけ単独で砕波
させることは不可能ではないか?
回答
一般的に2次波峯のみが単独で砕波するのはCollapsing型砕波の場合である.
この場合,主波峯との相互作用は行われず,2次波峯からジェットが放出されるため
,ジェットサイズはかなり小規模なものとなり,リーフによる波浪制御をする立場か
ら考えると,有効性が低いと言える.
同一条件下で2次波峯のみ単独で砕波させることが不可能と言うなら,換言すれば,
主波峯と2次波峯の干渉が起こっていることを指摘していることになる.
いずれにしろ,どのような流体メカニズムがこれら砕波形式の多様性に影響を及ぼ
しているのか解明することが今後の重要な課題である.
論文番号 13
著者名 安田孝志・陸田秀実・小笠原敏記・渡辺 敏・福本 正
論文題目 クノイド波の砕波後の変形・消波過程とジェットの関係
討論者 大野修史(東京工業大学)
質疑
図−2のジェットサイズと突入速度の関係についてこの図において突入速度は,UP
= [(DX/Dt)2+(DY/Dt)2]1/2 で表されているが,[DX/Dt]とジェットサイズの関係はど
うなるでしょうか?
回答
ジェット水平速度はジェット放出過程の平均値を求めました.その結果,砕波規模
が大きいほどジェット水平速度が大きくなることが分かりました.今後,トレーサー
等を使用して最大水粒子速度など詳細な検討を行く必要があると思います.
論文番号 14
著者名 合田良実、森信耕太、岡崎健一
論文題目 水平ステップ上の砕波限界に関する実験的研究
討論者 岩崎敏夫(東京久栄)
質疑
水平ステップ上の波浪変形に及ぼす影響は、非線形分散と周波数分散との作用によ
るので、この発表のように自由波と解釈している場合に、これを独立したものとして
扱うような印象を受け、やや理解しにくかった。しかし、きちんと分散を計算すれば
問題ないとのご
回答なので、その方向の研究を進められれば良いであろうと思う。
回答
今回対象にしたのは規則波の現象であるので、周波数分散は起きていない。非線形
分散の解釈はやや難しいが、基本波とそれに拘束された2倍、3倍周波数成分の波数
は非線形効果によって微小振幅波よりも短くなっている。それに対して、自由波であ
る2倍周波数成分は線形の分散関係式を満足している。この自由波とストークス波の
干渉によって、波形やフーリェ振幅の見かけの変化が出現すると考えられます。
論文番号 19
著者名 有川 太郎、磯部 雅彦
論文題目 非線形緩勾配方程式を用いた砕波判定法の適用性
討論者 大野修史(東工大)
質疑
「砕波限界にある定形進行波の鉛直加速度は1/2g」とあるが、定常流が角のある自
由表面を持つ場合には、角での鉛直加速度はたしかに、1/2gである。しかしこのよう
な場を砕波限界に対応させる論拠はあるのか?通常砕波発生時には、自由表面が角を
持つこともない。また、角をもった時に砕波する理由もないと思われるが?
回答
砕波限界を一種の極限波と考えると、角のある自由表面をもつ場合も極限波でとみ
なせるので、砕波限界に対応させて考えることができると思います。通常の砕波発生
時には、自由表面が角を持つことはない、というのは、巻き込みを伴うということで
しょうか、たしかに、巻き込みをともなうような場では、波形が多価関数になります
ので、巻き込んだ瞬間に圧力勾配は負になると考えることができると思います。
論文番号 21
著者名 辻本剛三
論文題目 乱流モデルによる砕波点近傍の流れの数値計算
討論者 二瓶泰雄(東工大)
質疑
この計算の枠組みでは、どこから渦度が生成されるのか?
図−5より表面近傍に渦度が集中しているが、表面において渦度生成を与える境界
条件になっているのか?
渦の不生不滅の法則より流体内部では渦度は生成されないことから、境界条件とし
てそれに対応するものを与えない限り、流れ場中には存在し得ない。もしそのような
境界条件を与えていないなら、本計算結果に多大な疑問が生じるが、この点に関して
詳細なコメントを頂きたい.
討論者 大野修史(東工大)
質疑
渦が強いシアの発生と言った実際の砕波帯の波動場において重要な乱れの発生過程
を考慮せずに解析を行うことには非常に問題があるのではないか?
回答
静止状態から波を発生させると乱れ等は壁面近傍にのみ見られ、流れ場全体には発
生しない。論文中のような乱れ等を発生させるためには、乱れのタネを計算領域に与
える必要があり、本計算ではk及びεに関しては適当な初期値を与えている.
具体的な初期値としては水の動粘性係数よりも小さくなるようにk及びε設定して
いる。但しk,εの組み合わせとしては無数にあるために本計算では主流部の流速の
0.1%程度のオーダーの乱れを与えている.この初期値は計算結果にかなり影響を
及ぼしているために、初期値に関しては検討する必要あり.
水面においては特別な境界条件を課してはいない。(論文に記載して通りである)
論文番号 22
著者名 灘岡和夫・大野修史
論文題目 水深積分型乱流エネルギーを連結させた砕波帯内波動モデルの提案
討論者 名古屋大学 喜岡 渉
質疑
水深積分型の1方程式乱流モデルをBoussinesq方程式と連立させて砕波減衰を求め
た例としてはKarambasらの研究があるが,彼らのモデルでは乱流モデルにおいて乱れ
の生成項PkをBoreモデルに基づき消散率をつりあうように(すなわち0方程式的に)
与えており,その扱いに疑問が残る.その点,本モデルに置いては大規模渦を循環を
用いて(物理性をもった形で)Pkを合理的に与えており,本モデルによる乱れの再現
性に興味を覚えるが,論文からはその優位性が明らかではない.Pkの与えかたは波高
減衰の再現性に大きく影響しないという指摘(Karambas)もあり,乱れエネルギーの
変動も含めて本モデルの優位性を具体的に示していただけないか.
回答
まず明確にしておきたいのはKarambasら(1992, Coastal Engineering, 18)のモデ
ルでは乱れの輸送方程式が用いられているものの,乱れを逐次解いているわけではな
い.彼らのモデルでは.経験式によって砕波区間を決定し,その区間において乱れが
Boreモデルにより定常的に生成されるものとしている.このような条件で周期平均さ
れた乱れの輸送方程式によって乱れの空間分布を得ている.得ている空間分布が固定
の条件であることから乱流モデルとしては1方程式ではなく,0方程式の枠組みだといえる.
将来的に漂砂等への応用を考えると位相分布を含めた乱れ強度の評価は重要となる
が,このような目的のためには,実際には非平衡である乱れの遷移過程を考慮して乱
れの輸送方程式を逐次解くことが合理的である.時間平均された定常な乱れを扱って
いるKarambasらのモデルでは乱れの位相分布を直接再現できない.また,Karambasら
のモデルでは砕波点が時間平均的にも変動を伴う不規則波の砕波過程も再現にも難が
あるが,本モデルでは不規則波の砕波過程も再現可能である.
また乱れのプロダクションについて,Karambasらのように乱れ場を定常として解く
場合にはプロダクションの見積もりが多少変わっても乱れの消散によって乱れの空間
分布はある程度一様になるように決定される.しかし本モデルのように乱れエネルギ
ーの非平衡性を考慮しようとする場合にはプロダクションの与え方によって乱れエネ
ルギーの時間的な変動が異なってしまうため,プロダクションのモデル化は一層重要
となる.
討論者 横浜国立大 岡安章夫
質疑
1.水深積分型の波動方程式+水深積分乱流モデルという枠組みについては Roelv
ink(1989)とどのように違うのか?
回答
1.Roelvink(1989, J. of Geophysical Res., Vol.94,)のモデルでは乱れ場を波
高分布(減衰)から求めているが,波動場は乱れ分布とは無関係に決定しており,波
動モデルと乱れ方程式がカップリングされた形にはなっていない.
質疑
2.乱れのソースとして水平渦が支配的ということだが,特に底質の巻き上げなど
については縦渦(斜降渦)が重要でこれは渦のストレッチに伴って乱流方程式で表さ
れるよりも速くより大きな乱れエネルギーを底面付近に運ぶという気がするが?
回答
2.物理過程としてはそのとおりである。ただし、そのモデル化となると、斜降渦
の発生・発達が連行気泡による浮力効果の関与も考えられる複雑な過程であることか
ら、その忠実な再現を目指したモデル化は、現時点では非現実的である。特に本研究
のような断面積分型のモデルでは、斜降渦のような局所的な3次元渦を直接表現する
ことは困難で、当面は、斜降渦の効果を拡散係数の増大のような形で表すことになる
と考えている。
論文番号 23
著者名 柿沼太郎, 渡辺 晃, 磯部雅彦
論文題目 三角形潜堤周辺の砕波を伴う波・流れ場の非線形数値計算
討論者 武若 聡 (筑波大学構造工学系)
質疑 (1)
潜堤背後の波向きの定め方について、本論分で対象とするような波の場 (不規則波
浪場ではない。) に方向スペクトルの推定方法を適用することは、原理的に誤ってい
ないでしょうか。ただし、特別なケースについては、妥当な結果が得られる場合もあ
るかと思います。以上の点に関する見解をお聞かせ願います。
回答 (1)
ここでは、分裂によって生じた倍周波数成分を含む波浪場を対象とし、EMLM (磯部
ら, 1984) を適用して方向スペクトルを推定しています。その際に必要な3種類の解
析データとして、ある同一地点における水平方向流速 u, v と水面変動の時系列を用
いました。波浪場の方向集中度が大きい場合、スペクトル解析により有限な解が得ら
れないことがあるでしょうが、今回は、周波数スペクトルのピークが複数個あること
や、潜堤上で波向が比較的複雑に変化した成分波が noise の役割をすること、そし
て、対象とするデータが数値解析結果として離散的な値で得られていることによって
、妥当な解が得られていると考えています。ただし、潜堤上のように非線形波が重合
している場合には、波と波との非線形干渉が生じるため、ここで用いた解析法は、適
用できないでしょう。
質疑 (2)
もしも可能でしたら、水位分布 (wave pattern) を図示したもの (例えば、図5上
のような形の濃淡パターンで。) をお見せ下さい。
回答 (2)
武若ら (1994) において、三角形潜堤による沿岸流の制御が扱われています。この
ように、潜堤を用いて波に伴う流れの制御を行なおうとする場合、平均水位の分布を
把握することは、重要な点の一つでしょう。柿沼ら (1997) の計算において、砕波帯
外に設置した三角形潜堤列が波を屈折及び分裂させ、沿岸流を概ね減少させています
が、平均水位を調べると、潜堤背後で沿岸方向に分布を持ち、この平均海面の傾きが
、場所によって、沿岸流を減少させたり、または、増加させたりする向きの流れを作
っていることが考えられます。更に、砕波帯内においては、砕波点の位置や set-up
等の沿岸方向の違いも、平均水位の沿岸方向の分布を形成する要因になります。こう
したことに関連して、服部先生 (中央大学) や權氏 (韓国水理研究所) からも示唆を
いただいており、次回、整理して報告したいと考えています。御
質疑ありがとうござ
いました。
参考文献
磯部・近藤・堀川 (1984): 方向スペクトルの推定における MLM の拡張, 第31回
海講論文集, pp. 173-177.
柿沼・渡辺・磯部 (1997): 三角形潜堤を用いた沿岸流の制御, 土木学会第52回年
講概要集, (II), pp. 66-67.
武若・入江・辻 (1994): テーパー型潜堤を用いた沿岸流制御の試み, 海岸工学論
文集, 第41巻, pp. 731-735.
論文番号 25
著者名 渡部 靖憲・森 憲広・稲垣 啓・佐伯 浩
論文題目 砕波帯内の平均流速場と流体運動スケールについて
討論者 二瓶 康雄(東工大)
質疑
乱流の微細構造,特にエネルギーのスペクトルなどについて議論するならば,DN
Sの3-Dシミュレーションを行う必要性があるが,2-Dシミュレーション結果だけ
で議論することに問題はないか.
回答
問題あります.乱流は本質的に3次元運動であり,2次元シミュレーションでは当
然表せません.3次元計算の結果が莫大な計算時間の増加のため今回の投稿の時点で
十分に検討できなかったため,まずは第一段階として2次元計算の結果を投稿したの
が実際のところです.弁解の様になりますが,本研究の主旨を確認したいと思います.
本論文においては,砕波帯内の乱れにおいて特徴的な慣性領域より低波数・低周波
数側の非等方乱れ,特にジェットの突入にともなう大規模渦近傍の周波数帯の特性を
明らかにすることを目的としました.砕波直後の大規模渦は2次元性を保持しており
,砕波後も乱れが十分に発達しほぼ等方と考えられる領域までは,この周波数帯にお
いては2次元性は多かれ少なかれ依然保持されていると考えられます(もちろん,斜
行渦の発生が確認されており,この周波数帯においても確かに3次元性を考える必要
はあります).この3次元流速場に関しては私も非常に興味を持っており,実験的に
調べましたが(Y.Watanabe, N.Mori, Three-Dimensional Characteristics of Veloc
ity Field and Effects of Undertow in a Surf Zone, Proc. 7th Int. Offshore an
d Porlar Eng. Conf., Vol. 3, pp.247 - 253, 1997.),モデル化する上で重要であ
る速度勾配を得ることが困難であるため,現在同様な数値計算手法により3次元に拡
張し,計算を行っております.この3次元シミュレーションの結果と2次元のものと
比較し,3次元性の生成機構を調べ,モデル化の上で必要な3次元性を抽出する目的
においても必要な研究であると考えております.
論文番号 27
著者名 仲座・津嘉山・川満・吉田
論文題目 巻き波型砕波に伴う流速場と底質の浮遊に関する研究
討論者 重松孝昌(大阪市立大学、工学部)
質疑
固定床実験で得た流速値を用いて砂移動のシミュレーションを行っているが、本来
は移動床実験によるデータを用いればならないと考えられる。固定床実験と移動床実
験による計測値はどの程度異なるのか。
回答
この質問は多分、「海の波は不規則だから規則波の実験でなく不規則波で行うべき
だ」という種のものと軸を一つにするものと思われます。本来ならば、先生がご指摘
のとおりのことをすべきでありましょう。しかし、移動床実験が非定常であること、
測定方法と測定に要する時間とを考えた時、もはや本手法による測定方法は役立たな
くなります。今後は、理想実験をより現実的なものにしていくことと、未解明な点を
少しでも開いていくことにしております。
現在のところ、「固定床実験と移動床実験による計測値はどの程度異なるのか」に答
えるようなデータを持っておりません。
論文番号 28
著者名 川村 育男,田中 仁,山路 弘人,アーマド・サナ
論文題目 非対称振動流の乱流遷移特性
討論者 服部昌太郎(中央大学 理工)
質疑
図ー4のfwc,fwc〜Rdについて質問します.大変興味深い結果と思いますが,何故
非対称流速時間波形の正流速時と負流速時の摩擦係数が異なるかを,お教えください.
回答
非対称振動流における摩擦係数は,峰における最大流速の絶対値Uc,峰位相,谷位
相のせん断力の最大値t0c,t0tを用いて,峰位相の摩擦係数fwc=2t0c/rUc2,谷位相
の摩擦係数fwt=2t0t/rUc2,と別々に定義したために,せん断力の峰と谷における最
大値の差異を反映して摩擦係数は異なる値を持つ結果となりました.
論文番号 31
著者名 黒岩正光・野田英明・芳地康征
論文題目 準3次元海浜流場の数値シミュレーションに関する研究
討論者 木村彰宏(京都大学大学院)
質疑
surface rollerによるせん断力の大きさはどのように評価したのですか.
波高の2乗に比例する形でということでしたが比例定数の取り方によって戻り流れの
大きさも変わってくると思うのですが.
回答
当日の討議(港研の栗山氏の質問)にもあったように,砕波帯内においては本来な
らsurface rollerに起因する付加的な運動量を考慮する必要と考えられるが,本研
究では,数値計算上,水面において何らかの境界条件を施す必要があるので,Svends
en(1984)の研究成果に基づきsurface rollerによる岸向きの運動量をshear stress
に置き換えて計算した.
比例定数は基本的には1程度であり,実験結果と一致するように与えている.
論文番号 32
著者名 信岡 尚道,加藤 始,三村 信男
論文題目 3次元海浜流モデル
訂正
}−5 のcross shoreとoff shoreの表記位置が逆です。
討論者 大野修史(東京工業大学)
質疑
砕波による効果をradiation stressのみで考えているが、実際の砕波現象との対応
に問題はないのか。そもそも、線形理論ででてくる波動流速分布は、砕波をともなう
ような非線形波の波動流速分布とは大きく異なっているはずである。radiaton stres
sの鉛直分布の重要さを述べてながら、元となる波動、流速の鉛直分布の見積もりを
線形理論によるのは問題ではないか。
回答
まず初めに、この論文では、radiation stressの評価精度について議論をしている
のではなく、3次元海浜流のdriving forceには、radiation stressの鉛直分布を用
いることが有効であることを主張していることを断っておきます。現時点での海浜流
理論には、まだこのレベルの議論が必要です。あと、著者はradiation stressという
言葉を、微小振幅波理論から求めるものだけでなく、一般的な波動成分の一周期残存
運動量の時間平均を指すものとして用いていることも断っておきます。
砕波によるジェットやsurface rollerの運動量はどうして生じるのでしょうか?。
本モデルでは砕波を、波が持っている運動量がジェットやsurface rollerの運動量に
移行する過程と捕らえています。したがって、砕波による波の運動量の減少分が、ジ
ェットやsurface rollerなどを含む流れの運動量になるだけで、「波と流れ(乱れ)
を合わせた運動量は保存される」と現象を捉えるべきであると主張します。radiatio
n stressは一周期平均したものであるが、その空間勾配は波の運動量の空間的な増加
や減少を示すものであり、上述の主張を一周期平均した形に対して表現できるもので
あります。
この論文で用いたradiation stressの評価は近似の低い方法で行っていることは著
者も認めます。但し、精度が非常に悪いとは考えておらず、第1次近似として線形理
論を用いた評価でも、相当に現象を表現できると考えています。線形理論での評価が
大きな問題と言うならば、これまでの微小振幅波理論で評価されたradiation stress
を用いた平均水位や流れの予測を否定することになると思います。しかし、これらの
計算でも、ある程度現象を表現できることは疑う余地はないはずです。
したがって、ここでの問題は、精度だけです。より精度を上げるには、radiation
stressをより高い近似(有限振幅性や
質疑者の主張する様に非線形性を考慮した波動
流速など)で評価すればよいです。評価方法は、今後の課題とさせて頂きます。
討論者 黒岩正光(鳥取大学・工学部)
質疑
計算における層数(鉛直方向)はどのようななっているか 層数を変えて計算した
場合、精度はあがるか
回答
最上面と最下面以外は各層の高さを一定としていますので、水深によって層数は異
なります。論文中に示した計算ケースは、層の高さを1cmとした場合です。砕波点付
近では7〜10層ぐらいであります。
層数を増やすことにより、radaiation stressの鉛直分布をより正確に表現できる
範囲では、精度が上がります。ただし、最上層では水位を変化させており、平均水位
の低下が最上層の初期の厚さより大きい場合などは計算が不安定になります。
討論者 浅野 敏之(鹿児島大学・工学部)
質疑
図−6の海浜流の8の字パターンは3次元的な流れとなっているのか ステップ地
形前面での湧昇流は再現されているのか
回答
実験では、染料を投入して観察した結果、8の字を描く流れのパターンが強く、二
つの円を描く流れのパターンより支配的でありました。計算では、8の字で交差して
いる範工学囲の流れの鉛直分布を確かめた所、上層と下層で流れの向きが異なってお
り、3次元的な流れであることを確かめています。但し、今回のステップ地形は開口
部の幅やスッテプの沿岸長さが現実的なものでないので、この流れのパターンが実際
の人工リーフ周辺で発生するかどうかは分かりません。
スッテプ開口部での堤体に向かう湧昇流は、水平流の混合を大きくして計算するこ
とで、再現できました。この混合は計算が不安定になるのを押さえるために与えたも
のですが、実際にこの範囲では構造物と波や流れの干渉により乱れが生じ、混合が生
じている可能性があると考えています。
論文番号 33
著者名 大熊義夫,阿部光信,田中正博,宇多高明
論文題目 高波浪時における波浪・海浜流場の現地観測に関する一考察
訂正
表−1の誤字があり,回帰年数ではなく回帰係数が正しい.
討論者 武浩 聡(筑波大学)
質疑
北向きの沿岸流が天妃山を迂回して発達したことを確認する材料として荒天時の天
妃山周辺の波浪場情報(砕波帯の分布他)があれば提示して頂きたい.また,天妃山
周辺の屈折計算を行えば砕波帯の分布,波高の分布などをある程度推定できるので沿
岸流が連続的に発達し得るのか否か考察できると思われます.
回答
残念なことに観測点の配置は,天妃山沖に設定していなかったとともに,天妃山を
挟んだD!< 0.4 m となり,ご指摘のように余り意味のない結果となります。しかし,分子粘性
ではなく,渦動粘性係数となれば,Lp ≫ 0.4 m でも十分に散逸効果が効いてきます
ので,ここで議論は意味を持つと考えています。勿論,そのような強い渦動粘性は砕
波を考えなければ説明できず,砕波の作用がここで扱っているように表層に留まって
いることは不自然さもあります。しかし,このようなモデル化によって変調不安定や
カオス的不規則化に及ぼす散逸効果を議論できるようになったことは確かです。この
モデルは実際の風波の発達過程を含めた伝播過程をモデル化しようとしたものではな
く,水の波の散逸系カオスの問題を極力シンプルに扱おうとしたものです。
論文番号 35
著者名 北野利一・中野 晋・大野嘉典・間瀬 肇
論文題目 複素表現を用いた非線形不規則波浪の統計解析
討論者 合田良実(横浜国立大学)
質疑
ご研究の結論の一つとして討議者の提唱したaltinessに問題があると指摘されてお
られますが,このパラメータは ! の統計的性質を吟味することを目的としたもの
ではありません.むしろ, " と # のskewnessが砕波帯内でほとんど同一の変化を
しているので,altinessが実用的には十分な意義を持っていると考えられます.
回答
確かに,今回のデータでの結果では $ と % のskewnessが砕波帯内でほとんど同
一の変化をしています.ところで,skewnessとは,確率密度関数の3次モーメントか
ら得られ,平均値を基準に分布の左右非対称性をみる,最も理解しやすい統計的代表
値です.しかし,ガウス過程から逸脱し,パルス化した波形に対しては,平均値周辺
の非対称性よりも平均値から非常に逸脱した確率の小さい(つまり,時系列上で局所
的な)部分に左右されます.準ガウス過程の波形に適用する時,分布形全体としてガ
ウス分布を基準に平均値周辺の確率の大きな部分の非対称性も含めて,確率密度関数
の非対称性をみることができ,大きな波形も小さな波形も,また,波形全体としての
前後非対称性を評価できるというのが我々の観点です.
また,線形不規則波がeta-xaiの位相面で統計的に大小の円を描くことを念頭に,
非線形不規則波が ( の位相面でいかなる図形を描くのかということが我々の主眼で
ある.非線形不規則波のeta-xaiの位相面で描く図形の特徴を記述するのに, & の両
軸に関してskewness, kurtosisを調べ, ' のskewnessが波の上下前後非対称性を表
わすことを今回の研究で明らかにしました.
論文番号 37
著者名 泉宮尊司,斉藤雅弘
論文題目 極値統計解析における順序統計量の分散を考慮した母数推定法
訂正
2ヶ所に校正ミスがあります。
181p.式(1)のべき乗のN-1をN-iに訂正。
181p.式(2)のべき乗のN-1をN-iに訂正。
討論者 合田 良実(横浜国立大学)
質疑
最小2乗法における課題であったデータの重み付けに対して理論的な裏付けがあり
,かつ使用に便利な方法を考案されたことに感謝いたします。つきましては母関数を
未知として最適合分布を選択する方式の場合に適用された場合のσ(XR)についても検
討頂けたならばありがたいと思います。データとしては,IHARのW.G.で使用した500標本のセットがあります。
回答
著者らの論文に対して,ご興味を示して下さり有り難うございます。ご質問の母関
数が未知な場合についても,いづれ時間を見つけて計算を行ってみたいと思います。
ただ,現在私が抱いている最大の疑問点は,いかにして最適合分布関数を見いだすか
であります。従来の方法では最大の相関係数をもつもの,あるいはAIC基準等によっ
ていますが,これらのみでは不十分であると思っております。たとえば,相関係数が
最も大きい基準は,数学的に言うならば必要条件であって,十分条件ではありません
。したっがて,相関係数が1となるような分布関数はいくらでも探すことができます
。また,得られたデータへの適合性がよいからといって,R年確率値を算定すると大
きな値であったり,あるいは逆の場合もあり得ると思います。したがって,私はデー
タとの適合性とR年確率統計値の変動特性の両方を考慮した判定法が良いのではない
かと考えております。現在,このことについて思案中ですので,結論が出せるように
なれば報告したいと考えております。
論文番号 38
著者名 山口正隆・大福 学・畑田佳男
論文題目 わが国沿岸における気象・海象要素の極値の再評価
討論者 合田良実(横浜国大 大学院工学研究科)
質疑
Jackknife法による分散推定には標本依存性があると思われますので,討論者の経
験公式による値と比べて小さく推定できるという結論を一般化することに問題がある
のでないでしょうか。
回答
モンテカルロシミュレーション結果の分析によれば,討議者の経験公式はとくに標
本数が小さい場合ほど分散(標準偏差)を過大評価するのに対して,jackknife法は
かなり高い精度(数%の誤差内)で分散(標準偏差)を推定しうることが明らかにな
っておりますので,実資料に対する解析結果もこの特性を反映していると考えており
ます。
論文番号 39
著者名 吉野真史,後藤智明
論文題目 物理因子重回帰モデルを利用した波浪追算について
訂正
(1) 図−2中の係数1.488は1.488×10−3が正しい.
(2) 式(5)中のiはIが正しい.
(3) 式(11)中のiはIが正しい.
討論者 駒口友章((財)漁港漁村建設技術研究所)
質疑
夏(7月)に特に追算精度が低下するという結果について,小さな陸風の影響がう
まく考慮できないからという考察となっているが本当にそうでしょうか.基本的に,
例えば波高が20cm(H1/3)以下のデータはCalmと扱われるのでデータの精度の低下と
も考えられるのではないでしょうか.
回答
波高がCalmの場合はデータ自体が無いため,波高の小さい場合の重回帰係数が比較
的波高が高いところへ引っ張られ,結果として精度が低下することは十分考えられま
す.しかしながら,7月の結果では波高よりむしろ周期を過小評価していることが大
きな問題点です.波形勾配が小さく,なおかつ陸風の場合に精度が低下するという現
象は状況証拠的に考えても,陸風下で風波からうねりに転じた波浪をうまく表現でき
ていないことが最大の原因と考えられます.
討論者 畑田佳男(愛媛大学工学部)
質疑
他の波浪推算結果を使った推算結果と推算結果の比較を行ってないか.行っていれ
ばその比較結果はどうか.
回答
単地点出力型スペクトル法との比較を行っております.今回の検討と異なり,風は
境界層モデルによる推算結果,メッシュ長は100kmの条件下で両者と比較しました.
結果,極大値は精度の差はそれ程見られませんが,発達時・減衰時の精度は物理因子
重回帰モデルの方が優っていました.
討論者 宇都宮好博((財)日本気象協会関西本部)
質疑
(1) 1987年にMT局が移設された.移設前のデータでモデルを作成し,移設後のデー
タでモデルの検証を行って問題はないのか.
(2) 将来,大阪湾の中央部で風が強くなるような風を組み入れてほしい(コメント).
回答
(1) 確かに問題はあります.しかしながら,1)移設距離が経度1.2',緯度0.6'と少
ないこと,2)移設前後でメッシュを組み直していること,3)フェッチの長い場合は,
フェッチに数%の誤差があっても係数に大きな影響はないこと,から問題は少ないと
考えます.
(2) 是非そうしたいです.できればデータ入手に御助力を賜れれば幸いです.
論文番号 42
著者名 中村聡志
論文題目 波のエネルギーとの干渉を考慮した長周期波数値シミュレーション
討論者 佐藤愼司(建設省土木研究所)
質疑
計算における沖側入射条件について,長周期波成分は入射させているのか?また,
比較に用いている実験では,(計算と同様に長周期波の造波を行っているのか?
回答
まずはじめに実験では,造波によって起きる自由長周期波を打ち消す造波制御は行
っていない.したがって,実験での水位記録の中にも造波開始から,波高は小さいけ
れども,自由長波が伝播する様子が記録されている.計算においては,Longue
t−Higgins・Stewart(1962)による入射波の波高で計算ウれる拘束波の水位変化・流速を与えている.
討論者 岡安章夫(横浜国立大学)
質疑
モデル,実験とも長周期波の反射率はほぼ100%と思われますが,現地海岸への
適用でもそれでよいのでしょうか.現地海岸での反射率等のデータがあればご紹介下
さい.
回答
実験では不透過な滑斜面を用いており,長周期波の反射率は非常に高い.計算では
,計算領域の端点で反射率を100%として与えている訳ではなく,段波の不透過滑
斜面への遡上・流下を計算しています.モデルの現地適用には,遡上流下時の摩擦や
砂中への浸透(将来)を考慮すれば良いと私は思います.現地海岸での長周期波の反
射率を計算していないので,今後発表していきたいと思います.
討論者 青木伸一(豊橋技術科学大学)
質疑
計算理論は拘束波から自由波へのエネルギー移行をどのような形で含んでいると考
えれば良いのでしょうか?
回答
波群に拘束された長周期波の波高(水位低下量)は,入射波群の高さによって決ま
ります.入射波群中の個々波の波高が浅水変形や砕波変形等によって変化すると,拘
束波の波高はそれに応じて変化します.入射波群の大きさによって決まる拘束波と比
較して不足するまたは過剰な長周期波の波高分が自由波になると考えています.
討論者 山口英一(中央大学大学院)
質疑1
今回の場合実験は断面水槽を用いたと予想されますが,数値計算を用いる式中で,
摩擦を底面のみでなく,側面も考慮する方が,正しい結果を導出すると思うのですが?
回答1
底面のみでなく,側面および内部の摩擦などの項を増やせば実験値とよく一致する
結果を得られると思います.しかし,そのような項を増やせば未知の係数(底面摩擦
中のfwの様な)が増えるので,今回はできるだけ任意性のある係数を使わないよう
にし,簡単な項のみを用いました.
質疑2
図−4の説明中にある図−2中の−9m,−10m,−11mにおける波群の峰の
位置の相違は砕波によってどの様にして起こるのでしょうか? また,それより岸側
では,どうしてよく一致しているのかを知りたいのですが.
回答2
図−2中の波の振幅の計算値と実験の入射波とを比較すると,砕波位置近く(−9
m,−10m,−11m)で実験の記録は1つの波群の中で前方に高い波高の波が集
中している傾向が強く現れているけれども,計算値にはそれが現れていない.この相
違は今回用いた砕波条件(簡便なエネルギー逸散の式)が実際の砕波前後の強よい非
線形を再現していないことによって起きる.
質疑3
潜堤の岸沖設置距離,入射波群の周期によっては,予想以上の遡上が起こる可能性
があるとありますが,その条件での実験,計算の比較を見てみたいと思いました.
回答3.
質疑4
図−4,11で実験値においてデータの取りはじめ直後に正の水位,もしくは負の
水位が見られますが,その解釈(どうして起きたのか)はどうとれば良いのでしょうか?
回答4
図を取り替えるべきでした.実際には指摘されたようなデータの取りはじめの水位
変化はありません.図−4,11はFFTを用いて実験値の長周期成分を抽出してい
ます.FFTを行う前に適当なウインドウをかけてデータの始点と終点をあわせてお
けばなくなります.
論文番号 43
著者名 松立 博樹・水口 優
論文題目 浅海域における波群の伝播変形と長周期波
討論者 不明
質疑
波群の偏平化に伴い負の自由波が発生するとあるが、波群の変形の仕方、例えば波
群が急峻化する場合に正の自由波が発生すると考えて良いのか。
回答
波群の形によるが、本研究で用いた単一波群については急峻化すると正の水位の自
由長周期波が発生する。外力項、あるいは水深の変化する場合、強制解(拘束長周期
波)の形も変化する。その差として自由長周期波が発生するものと考えられる。なお
、下記の論文の実験結果を見ると、浅水変形の効果により波群が急峻化した場合に自
由長周期波が発生していることが確認できる。正の波群の場合には正の水位の自由長
周期波が、負の波群の場合には負の水位の自由長周期波が発生している。
Nagase, S. and M. Mizuguchi(1996) "Laboratory experiment on long wave gene
ration by time-varying breakpoint", Proc. 25th ICCE, Orlando, pp1307-1320.
論文番号 44
著者名 青木伸一・喜岡 渉・山村易見・相川久紀・舟橋 香
論文題目 台風の通過に伴う沿岸長周期波の増幅と伝播に関する現地観測
討論者 岩崎敏夫(東京久栄)
質疑
台風の進路が海岸に近いので,結果の解釈をエッジ波等を関連させて将来検討され
てはいかがか?
回答
本研究では,長周期波が岸沖方向の重複波を形成していると仮定して反射率を求め
ていますが,ご指摘のように,沿岸域での長周期波の存在形態は大変複雑で,いろい
ろな可能性について検討する必要があると思います.エッジ波はその中でも重要な要
素であると著者らも考えており,沿岸方向の変化をみるために,97年度の実測では
波高計2台を汀線に平行方向に設置して観測しました.長周期波成分の空間分布を明
らかにするためには,数多くの波高計を用いた多点計測が必要で,決して容易ではあ
りませんが,いろいろな視点から観測データを見ていく必要があると思います.
討論者 森屋陽一(五洋建設技術研究所)
質疑
長周期波を自由波および拘束波と考えた入・反射分離は,具体的にどのようにして
計算されたのですか?
回答
本研究では,長周期波の伝播がほぼ岸沖方向に1方向とみなせる観測時間帯の水圧
波に対して,合田の線形理論による分離法を用いて入反射分離を行っています.長周
期波の個々の成分波の位相速度は線形理論より与えていますので,2次波である拘束
波の分離は正確には行えませんが,岸方向に向かう成分波の波速を各成分波の波速C
とした場合とすべての成分波の波速を短周期波のピーク周波数から求めた群速度Cgと
した場合の2種類について検討を加えました.群速度Cgを用いた結果では長周期波の
高周波数側で反射波のパワーがいくぶん小さくなりましたが,両ケースの分離結果に
は有意な差は見られませんでした.
論文番号 45
著者名 渥美他
論文題目 長周期波の港内侵入特性過程の現地観測と長周期波高予測式の検討
討論者 関本恒浩(五洋技研)
質疑
拘束波と自由波の分離を単一進行波と仮定して行われておりますが,多方向波浪場
の場合,単一方向波浪場に比べ拘束波は小さくなり,多方向波浪場では自由波を過大
評価する可能性があると思いますが,一次波の方向分布特性も含めた検討はされてま
すでしょうか.
回答
本検討は現場サイドの対策工の構築を早期に行うことが主目的なので,現地観測結
果と単一方向場として行ったシミュレーションが高相関だったのを確認して対策工の
検討を行った.一次波の方向分布特性も含めた検討は行われておりません.今後の検
討課題であります.
討論者 浜中建一郎(北海道東海大学)
質疑
発表中,この港の固有周期は10分程度であり,船体動揺の周期が2〜3分である
ことを考えると,港内の副振動は重要ではないとのことであるが,港内で長周期波は
多重反射波動場を形成しており,討論者(浜中)の解析によれば,周期2〜3分の入
射波のとき東水路に明確な重複波が発生し,問題の st.1 は節の位置となり,水平流
速は大となり船体動揺を引き起こしたものと考えられる.
回答
港内外の多点同時観測結果より,船体動揺の発生原因が港外より侵入した周期2〜
3分の長周期波であるのを確認した.副振動によると思われる増幅特性についても,
現場データを確認して検討している.現地では周期2〜3分の入射波に対しては,摩
擦の影響等によって明確な節と腹は現れにくい.したがって,st.1 が節の位置とは
確定できない.今後も引き続き観測を行い,流速分布についてもデータを収集したい.
論文番号 46
著者名 永井紀彦,橋本典明,白石 悟,川口浩二,清水勝義,上野成三,小林昭男
,東江隆夫,柴田孝雄
論文題目 現地連続観測による沖合長周期波の発達・減衰過程と港内係留船舶の動揺
討論者 青木伸一(豊橋科学技術大学)
質疑
港内で長周期波はトラップされるので,沖合観測記録だけから港内係留船舶の動揺
安全性を評価することは困難と思われる。
回答
ご指摘の通りと思います。しかし,沖合における波浪観測データの中から,長周期
波成分を抽出・整理しておくことは,問題解決のひとつの手がかりにはなると思いま
す。港外波浪(長周期波)と港内波浪(長周期波)との時間経過を含めた相関の解明
は,今後,個別の港湾毎にデータを蓄積しなければならないと考えております。
討論者 渥美洋一(北海道開発局)
質疑
苫小牧東港で必要とされている港内長周期波の予測に応用できるか?
回答
沖合長周期波パラメータ(m0L)のモニタリングは,有効であると思います。ただ
し,沖合長周期波諸元と港内の対象バース地点における長周期波諸元との時間経過を
含めた相関は,現地観測データをベースに整理しておく必要があります。
討論者 関本恒浩(五洋建設)
質疑
自由波と拘束波が共存する長周期波の方向スペクトルを求める場合のEMEP法の
適用限界を教えてほしい。
回答
EMEPにより長周期波の方向スペクトルを求める際の問題点として,長周期波の
周期と波長の関係を観測結果より経験的に求めている点が上げられる.これは,いわ
ゆる第一次近似的な推定法であるので,今後の研究テーマとして取り組む必要がある
と考えられる.
討論者 浜中建一郎(北海道東海大学)
質疑
港内の長周期波は複雑な重複波となっているため,節と腹の位置によって,その性
質が大きく異なったものとなる。このため,港内長周期波の特性を把握するためには
,1地点だけでなく多地点での同時観測を行うことが望ましい。
回答
ご指摘の通りと考えます。本論文では,特定のバースに限った係留船舶の動揺を検
討したわけですが,バースの位uが異なれば,当然,係留船舶の動揺は異なったもの
となると考えられます。なお一層の,観測データの蓄積を続けなければならないと考
えております。
論文番号 47
著者名 土田 充、灘岡和夫他
論文題目 多点観測による・・・
討論者 浜中建一郎(北海道東海大学)
質疑
港内で長周期波は多重反射波動場となっており、形成された重複波の節の位置で水
平流速は大(水位変動は小)となり、船体動揺を引き起こすと考えられる。従って、
防波堤の配置を変えるときは係船岸壁の位置が節とならないように考えるべきではな
いか?
回答
係船岸壁の位置が節の位置にならないようにすることが必要であることは認識して
おります。係船岸壁を節の位置にならないようにすることに着目して、なんらかの海
岸構造物を新設するとした場合には、今回対象としたバースだけでなく、港内のすべ
ての既設係船岸壁が節の位置にならないように設置しなければならず、これは非常に
困難であると考えています。そのため今回の検討では、改善案の一例として、比較的
小規模な海岸構造物でも港内の対象地域に侵入するエネルギーを減少させることがで
きることを示しました。この構造物により波高分布のパターンが変化し、位置により
稼働率が改善あるいは悪化するバースがあるが、港内の対象地域に侵入するエネルギ
ーを抑制すれば、港内全体としての稼働率は向上すると考えております。ただし、以
上の議論は波浪に注目していますが、本来は船体動揺自体に基づいて稼働率を議論す
る必要があり、現在船体動揺に基づいた検討をおこなっております。
論文番号 48
著者名 久保雅義、笹 健児、白石 悟、榊原繁樹
論文題目 数値計算手法が長周期波作用下における長周期船体動揺へ及ぼす影響について
討論者 合田良実(横浜国立大学)
質疑
船体係留問題の数値計算がここまで立派にできるようになったことに敬服します。
1)遅延関数法が理論的に優れていることは当然と思いますが、計算時間の負担は
どのようなものですか。
2)流体力を長周期で見積もると妥当な結果が得られるとの結論に賛成します。た
だ実測データに対してその手法を適用しなかったのは時間的制約によったのでしょうか。
回答
1)確かに遅延関数法は時間ステップごとに造波減衰力を畳み込み積分する必要が
あるため、ある周期での流体力係数(減衰係数)で代表させる運動方程式モデルより
も計算時間は長くなります。しかし計算機能力の発達により、遅延関数法による時系
列解析も時間的な負担はかなり軽減されています。参考までに今回の計算で見ますと
、時系列解析時間を1200秒間とした場合の計算時間は2〜3分程度であり、実用
上問題はないものと考えます。
2)流体力を長周期側で代表させた計算を行ったのは、係留船舶の長周期船体動揺
を表現する際には造波減衰力の運動方程式中での評価の仕方が極めて重要である旨、
現象を近似的に再現することを目的に実施いたしました。実測データの再現計算に考
慮しなかったのは、それぞれの動揺解析結果を足し合わせる計算方法が係留系の非線
形性を再現できないこと等によるものです。流体力係数一定型の運動方程式による解
析方法については、今後さらに検討する必要があると考えています。
討論者 新井信一(足利工業大学)
質疑
流体力固定法の計算を実施する場合、長周期波と有義波周期で分離して運動を計算
し、その後に合計の運動を算出するのは、係留系の非線形性がある場合には不適当に
なる。その場合は減衰力係数を係留系の固有周期の値として合計の運動を直接求める
方がより良い結果を与えると考えるが、いかがでしょうか。
回答
実測データとの詳細な比較を行う場合には、確かにご指摘のとおり足し合わせる方
法では非線形性の再現に問題があります。本研究では、運動方程式中での流体力係数
の取り込み方による、長周期船体動揺の再現現象を定性的に見る意味でこの計算を実
施いたしました。また係留系の固有周期で流体力係数を代表させるのが最も妥当であ
るとも考えます。本研究での計算例では、係留系の固有周期と長周期波の卓越周期が
ほぼ一致しており、その意味では係留系の固有周期で流体力係数を代表させて計算を
行ったとも言えます。ただし、両者の周期がかなり異なる場合では係留系の固有周期
で代表させた場合と長周期波の卓越周期で代表させた場合等の計算結果の比較も必要
と考えます。今後、ご指摘された条件等についても取り組んでみたいと考えておりま
す。
討論者 青木伸一(豊橋技術科学大学)
質疑
長周期運動の予測には造波減衰よりも、粘性減衰をいかに見積もるかが重要ではな
いか?
回答
ここでは、造波による減衰力と係留系のヒステリシスに起因する粘性減衰力の両方
を考慮して計算を実施しました。確かに長周期動揺時には造波減衰力はほとんどゼロ
に近くなりますので、粘性減衰力が主な減衰力となります。前後揺や左右揺に対する
粘性減衰係数は、現在500トンクラスの小型船の実験結果しか存在せず、本研究
でもこの係数を使用しました。ただし、数万トンクラスの船型による減衰力係数は現
在のところ不明な点が多く、今後実験等によって求める必要があります。そして船体
動揺計算にも正確に粘性減衰力を反映させていく必要があると考えています。
論文番号 49
著者名 山口正隆・畑田佳男・松木太郎
論文題目 ECMWF風を用いた長期波浪推算システムの適用性の検討
討論者 関本恒治(五洋建設株式会社 技術研究所)
質疑
1)ECMWF風を用いて推算した常時波浪は実測データを非常によく再現しております
が,極大値の再現性はいかがでしょうか。
2)累年平均波高の比較(図ー7)において佐多岬における推算値が大きいのは,地
形(陸地)の影響によるのでしょうか。
回答
1)極大値の再現性に関する検討は現在実施しているところでありますが,ECMWF風
は時空間解像度のうち,とくに時間解像度(6時間間隔)が低いので,勢力の強い台
風の場合には,台風モデルに基づく風を組み込むことを考えています。
2)波浪推算には,格子間隔5kmの大領域格子網と格子間隔1kmの小領域格子網を組み
合わせた2段階高地形解像度格子網を使用しておりますが,前面に種子島や屋久島な
ど複数の島々が位置する佐多岬では,依然として計算格子網の地形解像度が不足し,
推算値が観測値より大きくなっている可能性があります。
討論者 岡田弘三(日本気象協会 研究所)
質疑
1)波浪推算システムの適用性の検証であるから,定量的議論が必要である。推算波
高のRMSEはどの程度であろうか。
2)正確な計算を行うには,日本海の計算領域を拡げるべきである。
回答
1)気象庁波浪資料の観測間隔である3時間毎の9年間にわたる推算および観測波高
から得られたRMSE=[?{Hcal(i)-Hobs(i)}2/N]1/2と(累年平均波高)の概略値は,太
平洋岸北東部では0.61m(1.29m),太平洋岸南部0.47m(1.03m),東シナ海沿岸0.45
m(1.05m),日本海沿岸北部0.52m(1.10m),日本海沿岸西部0.45m(1.04m)であり
ます。もちろん,これらの値は個々の地点や対象期間ごとに変化します。
2)御指摘の通りです。そのため,北海道の北方海域にまで拡張した日本海波浪推算
用格子網を用意しておりますが,今回の論文では使用しておりません。ただし,北海
道の松前では,N方向を地形によって遮蔽されておりますので,計算領域の不足の影
響を受ける可能性は小さいと思われます。また,日本海ではNW方向の風が卓越します
ので,温海など他の地点の波浪に及ぼす影響もあまりないと考えております。
論文番号 50
著者名 平石哲也,河野信二,玉城重則,長谷川準三
論文題目 港湾構造物の設計に用いる長周期波の標準スペクトルについて
討論者 大成建設(株) 上野成三
質疑
提案された標準スペクトルは岸に向かう成分と沖に向かう成分の和と考えられる.
このスペクトルを持つ波が全て岸に向かう自由波と考えると,港に入射する長周期波
を過大評価することにならないか.
回答
沖で観測される長周期波は,岸へ向かう成分と沖へ向かう成分だけでなく,極端な
言い方をすれば多方向性を有していると考えることができます.もし,これらの多方
向性を明確に解析できるようになれば,長周期波を波向成分毎に分離して,港へ入射
させることも可能です.いまのところ,合成されたものとして長周期波の標準スペク
トルを考えていますので,指摘のとおり,若干過大評価になっていると考えられます.